Skip to content

1.3习题(证明题、变量代换)

期中考真题

微分学证明题

方程或方程组两边求导，联立求解 00a67d9fcee4b3340cd44300e87495d9.png

  1. 两边对t求导, 注意求导后是\(xf_x'(tx,ty)\), 两边乘t

  2. 隐函数问题。一阶偏导连续,所以\(f_2'(0,0)=f'_2(t,t^2)=-1/2\)

微分方程中的变量代换

题型一: 自变量替换

把\(z(x,y)\)替换成\(z(u,v)\). 实际上就是把\(\frac{\partial z}{\partial x}\)用\(\frac{\partial z}{\partial u},\frac{\partial z}{\partial v}\) 代替

注意偏微分没有链式法则。注意我们写的是一个因变量\(z\)，或者是写成\(f_1',f_2'\)这种形式，但实际上有两个变量。

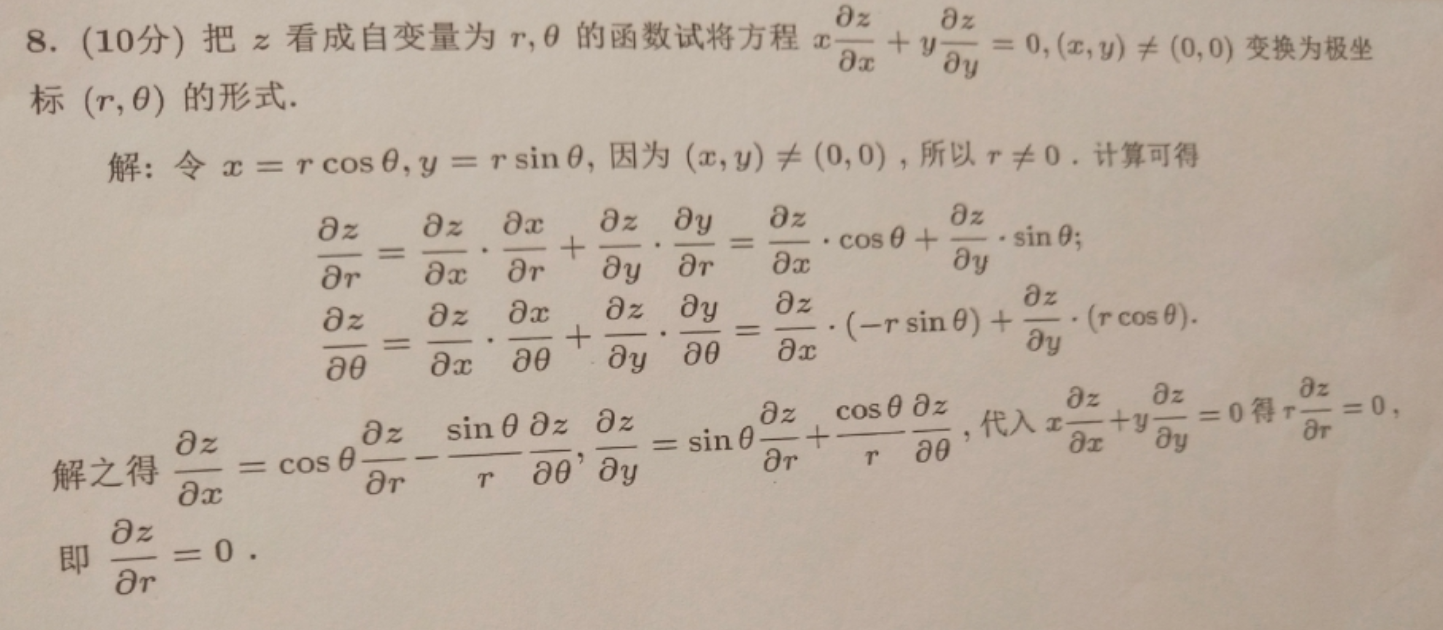
c56ca4b9b9120fa001d98885fee37270.png

题型二: 变换函数和自变量

习题8-3 14

其他

  1. \(u=x^{y^z}\) 偏导

注意是\(x^{(y^z)}\). 先算上面的

\(\ln u=y^z\ln x \rightarrow \frac{1}{u}\frac{\partial u}{\partial y}=zy^{z-1}\ln x\)

求\(d^k(e^x\sin y)\)

法一:

\(z=f(x,y)\)

\[ d^n z=\sum_{k=0}^n \binom{n}{k}\frac{\partial^k z}{\partial^k x \partial ^{n-k}y}dx^kdy^{n-k} \]

先对\(x\)求导不变，然后对y\(\frac{\partial^k x}{ \partial ^{n-k}}=e^x (\sin y)^{(k-i)}=e^x\sin(y+\frac{\pi}{2}(k-i))\)

法二:

设\(d^k(z)=e^x(a_k\cos y+b_k\sin y)\)

1aee9566e967609f050dc755d87a71a1.png

e053597ae529bd74b412785fb27ce867.png

答案 题号7: 这种题目一般要带着括号里的自变量写，不容易搞错。(1)式子要代入x=0才能得到\(f_1'(1,1)\). (2)式子要代入\(x=1\)

2656fb2f2355e973090b748b75a962c3.png

题号8:

不需要计算an,bn的表达式，给傅里叶级数的式子里代入x求值。记得减去\(\frac{a_0}{2}\)

Comments