Lec1 AVL,Splay
Lec1: AVL+Splay
AVL
定义
\(h(x)\): 以\(x\)为根的子树的最大深度 - 空树\(h=-1\) 单个点\(h=0\)
平衡因子 \(BF(x)=h(lson(x))-h(rson(x))\) 一棵满足条件的AVL树 \(\forall x, BF(x) \in \{-1,0,1 \}\)
复杂度分析
设最大深度为k的树的最少节点数为\(h_k\),则\(h_{k+1}=h_{k}+h_{k-1}+1\) 类似斐波那契数列可以得到\(h_n=O(c^n)\)
也就是说树高是\(O(\log n)\)的
操作
旋转
旋转是AVL和splay的基础,它能在不改变一棵合法 BST 中序遍历结果的情况下改变局部节点的深度。
以根节点为视角,旋转分为左旋和右旋:(图片来自OI-wiki)
以儿子节点为视角,就可以不用区分左旋和右旋。实际上旋转是把孩子和父节点交换但保持BST性质的操作,左儿子交换上去叫右旋,右儿子交换上去叫左旋。
这样我们可以统一写出旋转操作的代码:
int chk(int x){return rson(fa(x))==x;}
void rotate(int x){
//把x换到父亲的位置
int y=fa(x),z=fa(y),k=chk(x),w=tree[x].ch[k^1];
tree[y].ch[k]=w;
fa(w)=y;
if(z) tree[z].ch[chk(y)]=x;
fa(x)=z;
tree[x].ch[k^1]=y;
fa(y)=x;
pushup(y);
pushup(x);
}
插入
插入一个点后,可能会破坏关系。称插入的点为Trouble maker,递归向上找到的第一个不满足关系的点为trouble finder
LL Rotation: 把B换到A的位置
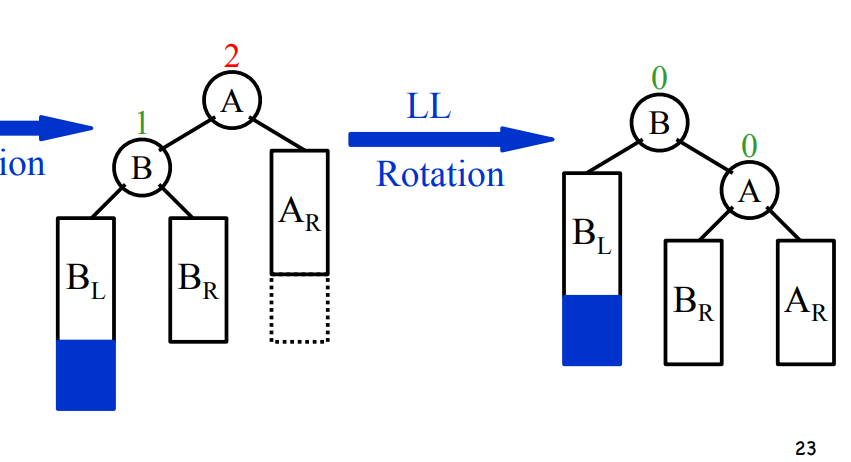
trouble finder是A, 插入点在B的左儿子子树中(也有可能是那个点)
LR Rotation:CB互换,CA互换
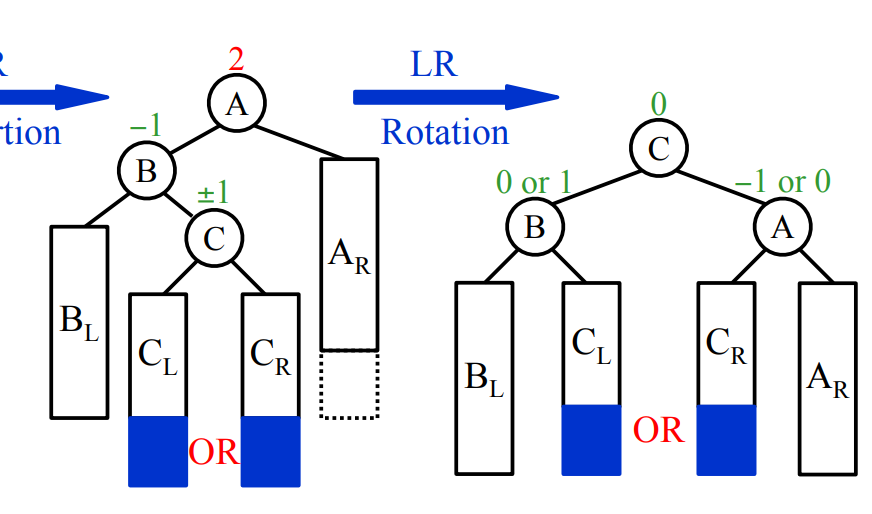
void maintain(int x){
if(abs(h(lson(x))-h(rson(x)))>=2){//如果>=2
if(h(lson(x))>h(rson(x))){
if(h(lson(lson(x)))>h(rson(lson(x)))){
rotate(lson(x));//LL single rotation
}else{
rotate(rson(lson(x)));//LR double rotation
rotate(lson(x));
}
}
//... 右节点的情况对称
插入: 先按照BST插入节点,接着向上,找到第一个不满足AVL操作的点,消除这个点即可。因此AVL插入的rotate次数≤2
Info
Code
#include<bits/stdc++.h>
#define T int
#define fa(x) ((x)->fa)
#define lson(x) ((x)->ch[0])
#define rson(x) ((x)->ch[1])
struct AVL{
struct node{
T val;
int h;
node* ch[2];
node* fa;
int siz;
int dir(){
if(!fa) return 0;
return fa->ch[1]==this;
}
void push_up(){
siz=1;h=0;
if(ch[0]){
siz+=ch[0]->siz;
h=std::max(h,ch[0]->h);
}
if(ch[1]){
siz+=ch[1]->siz;
h=std::max(h,ch[1]->h);
}h++;
}
node(T val=0,node* _f=0):val(val),h(1),siz(1){
ch[0]=ch[1]=NULL;
fa=_f;
}
};
int height(node* x){
return x!=NULL?x->h:0;
}
node* root;
void connect(node *x, node *fa, int k) {
if(x != NULL) x->fa = fa;
if(fa != NULL) fa->ch[k] = x;
else root=x;
}
void rotate(node *x) {
//rotate x to its parent's position
node* y = fa(x);
node* z = fa(y);
int yson = x->dir(); //the branch of x, 0 is left, 1 is right
if(z == NULL) {
root = x;
x->fa=NULL;
} else {
int zson = y->dir();
connect(x, z, zson);
}
connect(x->ch[yson^1], y, yson);
connect(y, x, yson^1);
y->push_up();
x->push_up();
}
int get_rank(T v, node* x) {
if(x == NULL) return 0;
if(v <= x->val) return get_rank(v, lson(x));
int lsiz = (lson(x) != NULL ? lson(x)->siz : 0);
return lsiz + 1 + get_rank(v, rson(x));
}
int get_rank(T v) {
return get_rank(v, root);
}
T get_prev(T v) {
node *x = root;
T ans;
while(x != NULL) {
if(x->val < v) {
ans = x->val;
x = rson(x);
} else {
x = lson(x);
}
}
return ans;
}
T get_succ(T v) {
node *x = root;
T ans;
while(x != NULL) {
if(x->val > v) {
ans = x->val;
x = lson(x);
} else {
x = rson(x);
}
}
return ans;
}
T kth(int k, node* x) {
if(!(lson(x))) {
if(k == 1) return x->val;
return kth(k-1, rson(x));
}
if(k <= lson(x)->siz) return kth(k, lson(x));
if(k == lson(x)->siz + 1) return x->val;
return kth(k - lson(x)->siz - 1, rson(x));
}
T kth(int k) {
return kth(k, root);
}
void solveAVL(node *x) {
while(x != NULL) {
x->push_up();
if(abs(height(lson(x))-height(rson(x))) <= 1) {
x = fa(x);
} else {
node* p;
if(height(lson(x)) > height(rson(x))) {
p=lson(x);
if(height(rson(lson(x))) > height(lson(lson(x)))){
p=rson(lson(x));//LR rotation
rotate(p);
}
rotate(p);
} else {
p=rson(x);
if(height(lson(rson(x))) > height(rson(rson(x)))){
p=lson(rson(x));//RL rotation
rotate(p);
}
rotate(p);
}
x=fa(p);
}
}
}
void insert(T val){
node* x=root;
node*fa=NULL;
while(x){
// x->siz++;
fa=x;
if(val<x->val) x=lson(x);
else x=rson(x);
}
x=new node(val,fa);
if(!fa) root=x;
else if(val<fa->val) fa->ch[0]=x;
else fa->ch[1]=x;
solveAVL(x);
}
void del( T val){
node* x=root;
while(x){
// x->siz--;
if(x->val==val) break;
if(val<x->val) x=lson(x);
else x=rson(x);
}
if(!x) return;
if(lson(x)&&rson(x)){
node* y=rson(x);
while(lson(y)) y=lson(y);
x->val=y->val;
x=y;
}
node* fa=fa(x);
node* son=lson(x)?lson(x):rson(x);
if(fa){
if(fa->ch[0]==x) fa->ch[0]=son;
else fa->ch[1]=son;
}else root=son;
if(son) son->fa=fa;
solveAVL(fa);
}
};
int main() {
//freopen("P3369_4.in","r",stdin);
AVL Tree;
int n;
scanf("%d",&n);
while(n--) {
int op, x;
scanf("%d%d",&op,&x);
if(op == 1) {
Tree.insert(x);
} else if(op == 2) {
Tree.del(x);
} else if(op == 3) {
printf("%d\n",Tree.get_rank(x)+1);
} else if(op == 4) {
printf("%d\n",Tree.kth(x));
// cout << Tree.kth(x) << endl;
} else if(op == 5) {
printf("%d\n",Tree.get_prev(x));
// cout << Tree.get_prev(x) << endl;
} else {
printf("%d\n",Tree.get_succ(x));
// cout << Tree.get_succ(x) << endl;
}
// printf("debug:%d\n",Tree.root->val);
// Tree.checkNodeSize();
}
return 0;
}
Splay
定义
操作
核心思想:操作某个点时(查询、插入、删除),就通过旋转将目标点转移到根部
splay
两种情况:
void splay(int x,int goal=0) { //把x转到goal的子节点,goal默认=0的时候转到根
while(tree[x].fa!=goal) {
int y=tree[x].fa;
int z=tree[y].fa;
if(z!=goal) {
if(chk(x)==chk(y)) rotate(y);//zig-zig
else rotate(x);//zig-zag
}
rotate(x);//如果z就是根,那么只需要zig一次
}
if(!goal) root=x;
}
}
Code
#include <iostream>
#define MAXN 100000
#define INF 0x3f3f3f3f
using namespace std;
struct Splay{
struct node{
int fa;
int ch[2];
int val;
int cnt,sz;
}tree[MAXN+5];
int root;
#define fa(x) (tree[x].fa)
#define lson(x) (tree[x].ch[0])
#define rson(x) (tree[x].ch[1])
#define h(x) (tree[x].h)
void pushup(int x){
tree[x].sz=tree[lson(x)].sz+tree[rson(x)].sz+tree[x].cnt;
}
int chk(int x){
return rson(fa(x))==x;
}
void rotate(int x){
//x->fa
int y=fa(x),z=fa(y),k=chk(x),w=tree[x].ch[k^1];
tree[y].ch[k]=w;
fa(w)=y;
if(z) tree[z].ch[chk(y)]=x;
fa(x)=z;
tree[x].ch[k^1]=y;
fa(y)=x;
pushup(y);
pushup(x);
}
void splay(int x,int goal=0){
while(fa(x)!=goal){
int y=fa(x),z=fa(y);
if(z!=goal){
if(chk(x)==chk(y)) rotate(y);
else rotate(x);
}
rotate(x);
}
if(!goal) root=x;
}
int newNode(int val){
static int cnt=0;
tree[++cnt].val=val;
lson(cnt)=rson(cnt)=0;
tree[cnt].cnt=tree[cnt].sz=1;
// tree[cnt].h=0;
return cnt;
}
void find(int val) { //鎵惧埌鏈€澶х殑<=val鐨勬暟骞舵妸瀹冭浆鍒版牴
if(!root) return;
int cur=root;
while(tree[cur].ch[val>tree[cur].val]&&val!=tree[cur].val) {
cur=tree[cur].ch[val>tree[cur].val];
}
splay(cur);
}
void insert(int val) {
int cur=root;
int f=0;
while(cur&&tree[cur].val!=val) {
f=cur;
cur=tree[cur].ch[val>tree[cur].val];
}
if(cur!=0) {
tree[cur].cnt++;//涓嶇敤push_up鍥犱负splay涓凡缁弍ushup杩囦簡
} else {
cur=newNode(val);
if(f) tree[f].ch[val>tree[f].val]=cur;
tree[cur].fa=f;
}
splay(cur);
}
int get_val(int k) {
int x=root;
while(1) {
if(lson(x)&&k<=tree[lson(x)].sz) {
x=lson(x);
} else if(k<=tree[lson(x)].sz+tree[x].cnt) {
return tree[x].val;
} else {
k-=tree[lson(x)].sz+tree[x].cnt;
x=rson(x);
}
}
return 0;
}
int get_rank(int val) {
find(val);
if(tree[root].val<val)
return tree[lson(root)].sz+tree[root].cnt+1;
return tree[lson(root)].sz+1;
}
int _pre(int val) { //娉ㄦ剰杩斿洖鐨勬槸浣嶇疆鑰屼笉鏄€?
find(val);
if(tree[root].val<val) return root;
int cur=lson(root);
while(rson(cur)) {
cur=rson(cur);
}
return cur;
}
int pre(int val) {
return tree[_pre(val)].val;
}
int _nex(int val) {
find(val);
if(tree[root].val>val) return root;
int cur=rson(root);
while(lson(cur)) {
cur=lson(cur);
}
return cur;
}
int nex(int val){
return tree[_nex(val)].val;
}
void del(int val) {
int pre=_pre(val),nex=_nex(val);
splay(pre);
splay(nex,pre);
int del=lson(rson(pre));
if(tree[del].cnt>1){
tree[del].cnt--;
splay(del);
}else lson(nex)=0;
}
}T;
int n;
int main() {
int opt,x;
scanf("%d",&n);
T.insert(-INF);
T.insert(INF);
for(int i=1;i<=n;i++){
scanf("%d %d",&opt,&x);
// printf("ok %d %d\n",opt,x);
switch(opt){
case(1):{
T.insert(x);
break;
}
case(2):{
T.del(x);
break;
}
case(3):{
printf("%d\n",T.get_rank(x)-1);
break;
}
case(4):{
printf("%d\n",T.get_val(x+1));
break;
}
case(5):{
printf("%d\n",T.pre(x));
break;
}
case(6):{
printf("%d\n",T.nex(x));
break;
}
default:{
break;
}
}
}
}
势能分析
让消耗大的那一步操作势能减小
multipop
有一个栈,两种操作 - Push 进去1个元素,消耗1时间 - 每次可以选择 Pop k个元素(只要栈里有),消耗k时间。 现在一共有n 个元素,问经过一系列合法操作之后总共消耗多少时间。
让消耗大的操作势能减少, 那么pop k的消耗比较大, 势能应该变小. 所以定义\(\Phi(S_k)\)代表此时栈中的元素个数。 最后栈中元素可能有0~n个,故\(\Phi(S_n) \geq \Phi(S_0)\)满足势能分析的条件
- push \(a_i=1, \Phi_i-\Phi_{i-1}=1\)
- pop \(a_i=k, \Phi_i-\Phi_{i-1}=-k\)
所以总时间\(\sum( a_i+\Phi_i-\Phi_{i-1}) \leq 2n\)
std::vector
如果有空位,就插入。否则新建一个大小为原来2倍的表,把原有元素复制进去. 假设最后表是满的
复制的操作对应势能减小。可以设势能为表中的空位个数的相反数 开始时为-1,最后为0,满足放缩条件。 - 情况1 \(a_i=1, \Phi_i-\Phi_{i-1}=1\) - 情况2 \(a_i=k, \Phi_i-\Phi_{i-1}=(-k)-0=-k\)
总时间\(O(n)\), 平均下来每次是\(O(1)\)
Splay
定义势函数
\(Size(i)\)为i子树的大小. 为了方便,定义\(rank(i)\)为子树大小取对数
