Skip to content

9.Relation

注意看关系的定义，计数不同性质关系(reflexive,symmetric,antisymmetric)的, 偏序关系

Definition

A binary relation from \(A\) to \(B\) is a subset of \(A\times B\)

The graph of function \(f:A \to B\)is a relation. 但反之不成立

A relation on a set A is a relation from A to A

A relation can be expressed as

  • Connection matrix \(m_{ij}=[(a_i,b_j)\in R]\) 可以理解成图的邻接矩阵,只有0和1
  • Directed graphs

Properties

Properties Definition Connection Matrix Digraph
reflexive \(\forall x\in A,(x,x)\in R\) 对角线全为1 每个结点都有自环
irreflexive \(\forall x\in A,(x,x)\notin R\) 对角线全为0 每个结点都没有自环
symmetric \(\forall x,y\in A,(x,y)\in R \to (y,x) \in R\) \(M=M^T\) 每一条边都有反向边
antisymmetric \(\forall x,y\in A,((x,y)\in R\wedge(y,x)\in R)\\ \to x=y\) 对角线可以为0/1, 非对角线上的对称位置不能同时为1 每一条边都没有反向边，可以有自环
asymmetric \(\forall x \in A,(x,y)\in R\to(y,x) \notin R\) 对角线全为0,非对角线上的对称位置不能同时为1 每一条边都没有反向边,不能有自环
transitive \(\forall x,y,z\in A ((x,y)\in R\wedge (y,z)\in R)\\ \to(y,z)\in R)\) \(M^2 \vee M=M\) 对于每一条从\(u\)到\(v\)长度为2的路径，有一条边\((u,v)\). (即\(R^2\subseteq R\))
  • 也就是说如果\((x,y) \in R且x\neq y\)则\((y,x)\notin R\) . 如果R是antisymmetric的，那么可以包括(a,a).

A relation can be both symmetric and antisymmetric: \(M=\begin{pmatrix}&1 \ &0\\&0 \ &1 \end{pmatrix}\)

symmectric+transitive=reflexive?

No, for example \(M=0\)

错在symmetric不代表对于任意的\(a\)都存在\(b\)使得\((a,b)\in R\)

Counting relations on set

|A|=n, how many relation on set A is

  • reflexive: \(2^{n^2-n}\)
  • symmetric: \(\color{red}2^{(n^2-n)/2}\times 2^n=2^{(n(n+1)/2)}\) 注意对角线上可以是0或1
  • antisymmetric: \(\color{red}3^{n(n-1)/2}\times 2^n\) 对于矩阵非对角线上的一对对称的元素, 只能是(0,0),(0,1),(1,0). 对角线上可以是0或1
  • asymmetric \(3^{n(n-1)/2}\)，对角线上全为0

Operations

\(R^{-1}=\{(b,a)|(a,b)\in R \}\)

\(M_{R^{-1}} =M_R^T\)

\(S\circ R=\{(a,c)|(a,b)\in R \wedge \color{red}(b,c)\in S\}\)

注意顺序，S在后面！！！！

对应邻接矩阵的乘法(用与运算代替乘法，或运算代替加法)

\[ M_{S\circ R}=M_R \times M_S \]

\(R^n=R\circ R \circ \dots R\)

或者对应有向图中长度小于等于n的路径(Floyd传递闭包（确信))

The relation R on a set A is transitive if and only if \(R^n \subseteq R\) for n = 1, 2, 3,...

Closures

If there is a relation S with property P containing R, such that S is a subset of every relation with property P containing R, then S is called the closure of R with respect to P

证明分3步

  • \(R \subseteq S\)

  • \(S\) 满足性质\(P\)

  • 证明S是最小的，可以反证，或者证明任意一个满足P的关系都包含S

    image-20230530095535513

reflexive closure: \(R\cup I_a\)

symmetric closure:\(R \cup R^{-1}\)

transitive closure: \(\cup_{i=1}^{\infty} R^i\)

Warshall's Algorithm

手算，每次取第k行和第k列. 用第k列(a[i][k])和第k行a[k][j]两两匹配,如果有2个都是1的,就把a[i][j]设为

Equivalence Relations

reflexive,symmetric and transitive-> equvalence relation

Equivalence class

Equivalence class of \(x\): \([x]_R\) or \([x]\) The set of all elements that are related to an element \(x\)

Eg. \(R=\{(a,b)|a \equiv b\pmod 3\}\)

\([0]=\{3k|k \in Z\},[1]=\{3k+1|k \in Z\},[2]=\{3k+2|k \in Z\}\)

Partitions of a set and Relations

Theorema71d20e55427d08766a69c287943dd0f.png 左推右很好证。考虑右推左

\(R=\{(a,b)|a,b \in A_i\}\) \(pr(A)=A_1,A_2\dots A_n\)

  • reflexive: \(\forall a \in A,\existssss A_i, a \in A_i\)
  • symmetric
  • transitive: \(aRb,bRc\), \(a,b\in A_i\ \ b,c \in A_j\). because \(A_i \cap A_j=\emptyset(i \neq j)\), so \(i=j\)

4a48fe0446513dfdb3c3cc67cb93c5e7.png

\(|A|=n\), how many different equivalence relations on the set \(A\) are there

Consider the partition of A. \(\sum_{k=0}^n S(n,k)\)

Operation of equivalence relations

\(R_1,R_2\) is equivalence relation, \(R_1 \cup R_2\) is not

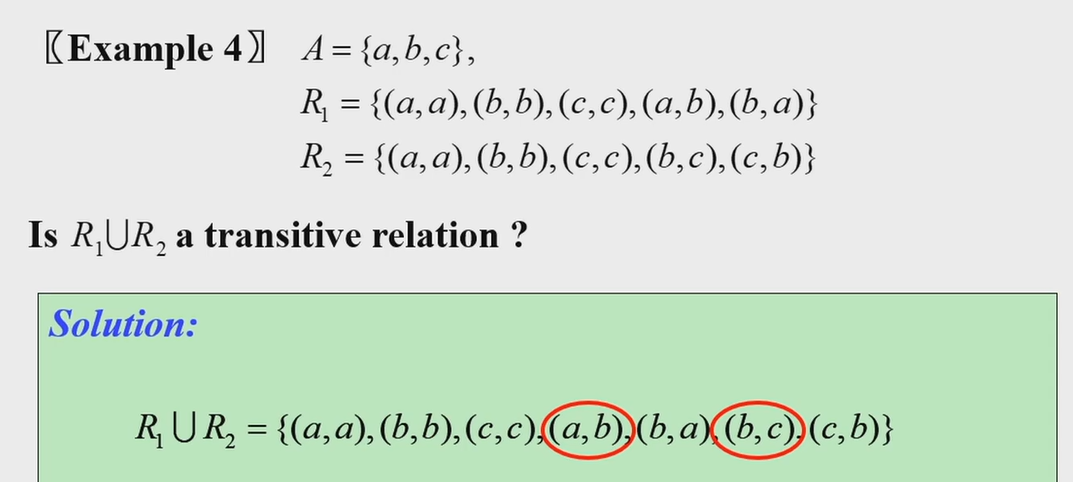
ee1f7479a56640ef06df0847fd708fda.png

因为不满足Transitive, 对\(R_1 \cup R_2\) 再跑传递闭包就可以

Partial Orderings

a reflexive,antisymmetric and transitive relation is a partial order.

  • 验证是partial order,前两项容易，注意transitive relation要枚举3个点

S is a set, R is a partial order on S, \((S,R)\) is called a poset

The elements a and b of a poset \((S, \leq)\) are called comparable if either \(a \leq b\) or \(b \leq a\). (这里的≤代表抽象的大小关系，不是实数的比大小)

If \((S, \leq )\) is a poset and every two elements of S are comparable, S is called a totally ordered or linearly ordered set, or a chain.

Hasse Diagrams

先把偏序关系表示成有向图，根据传递性去掉不需要的边。再分层画出节点，去掉箭头。

5ceac7f835e6d568a49b66c276c061ae.png

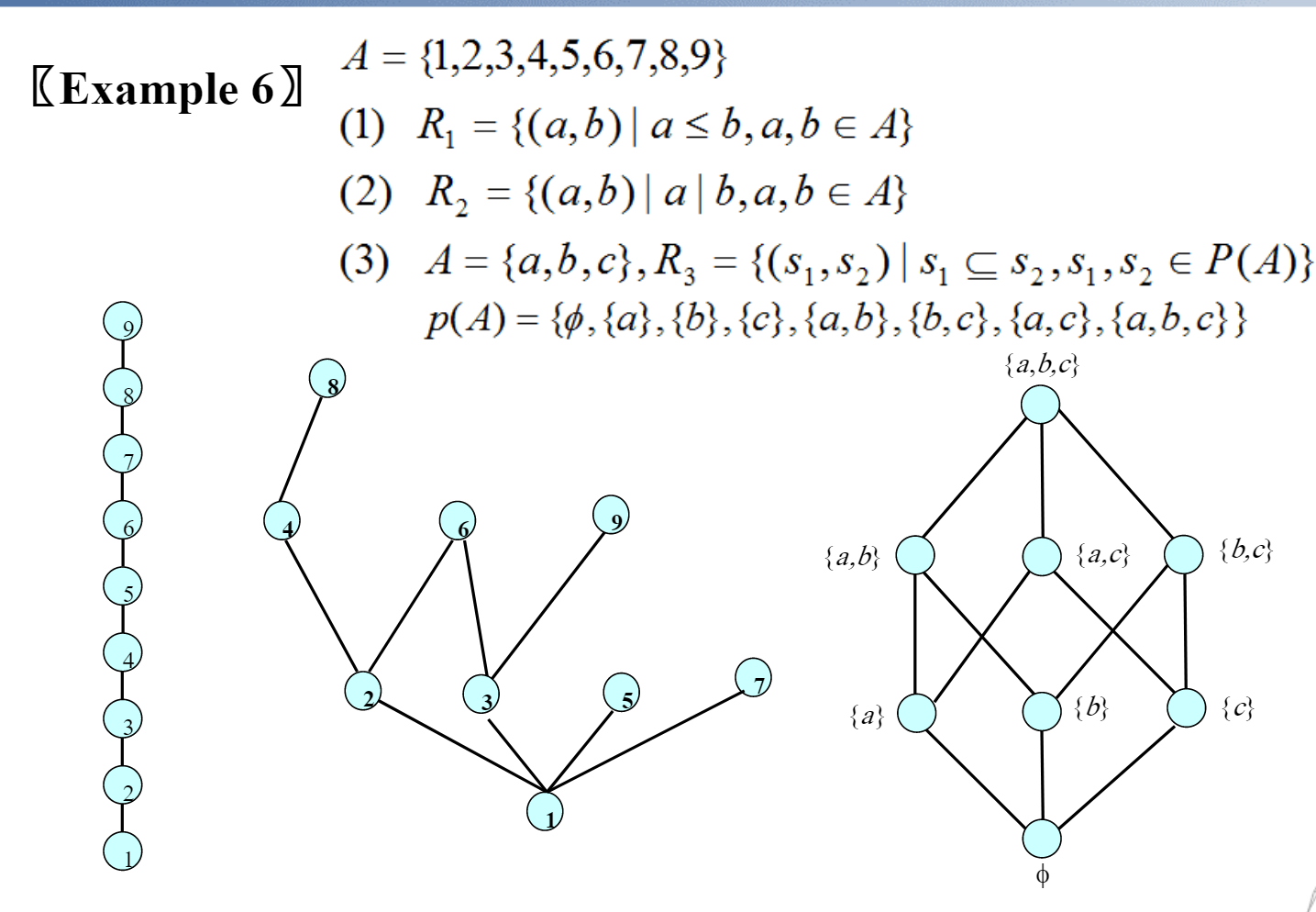
5d015e38a865247e1e8f11417b8973cb.png

画\((A,|)\)的Hasse diagram，可以不必用通用的方法

  1. 如果有1,则1在最底部
  2. 接下来一层是质数
  3. 依次放上质数的倍数

Chain and antichain

A subset of a poset is called a chain if every two elements of this subset are comparable.

A subset of a poset is called an antichain if every two elements of this subset are incomparable

Dilworth's theorem:

every finite poset can be partitioned into k chains, where k is the largest number of elements in an antichain in this poset

Special Elements

  • maximal element \(m\): 不存在\(a \in S,a \geq m\) （可能有多个，也可能不存在) (top element of Hasse diagram)

  • minimal element: (bottom element of Hasse diagram)

  • greatest element: \(\forall a \in S,m \geq a\) (唯一)

  • least element: (唯一)

  • upper bounds: for \(A \subseteq S\), \(\existssss a, \forall b \in A, a \geq b\), then \(a\) is upper bound of \(A\)

    • least upper bound(lub)

  • lower bounds

    • greatest lower bound(glb).

165b7177d8e14eb3fc8d55cce93fc393.png

Lattice

a poset is called a lattice if each pair of elements have a glb and lub.

every totally ordered set is a lattice

\((Z^+,|)\) is a lattice. (glb=两个数的最大公因数，lub=最小公倍数) \((P(S),\subseteq)\) is a lattice (取并集、交集)

Well-ordered set

a well-ordered set is a poset that every nonempty subset of A has a least element. a well-ordered set is a totally ordered set.(choose subset of size 2)

mathmatical induction(见Section 5)

Topological Sorting

Comments