VFN

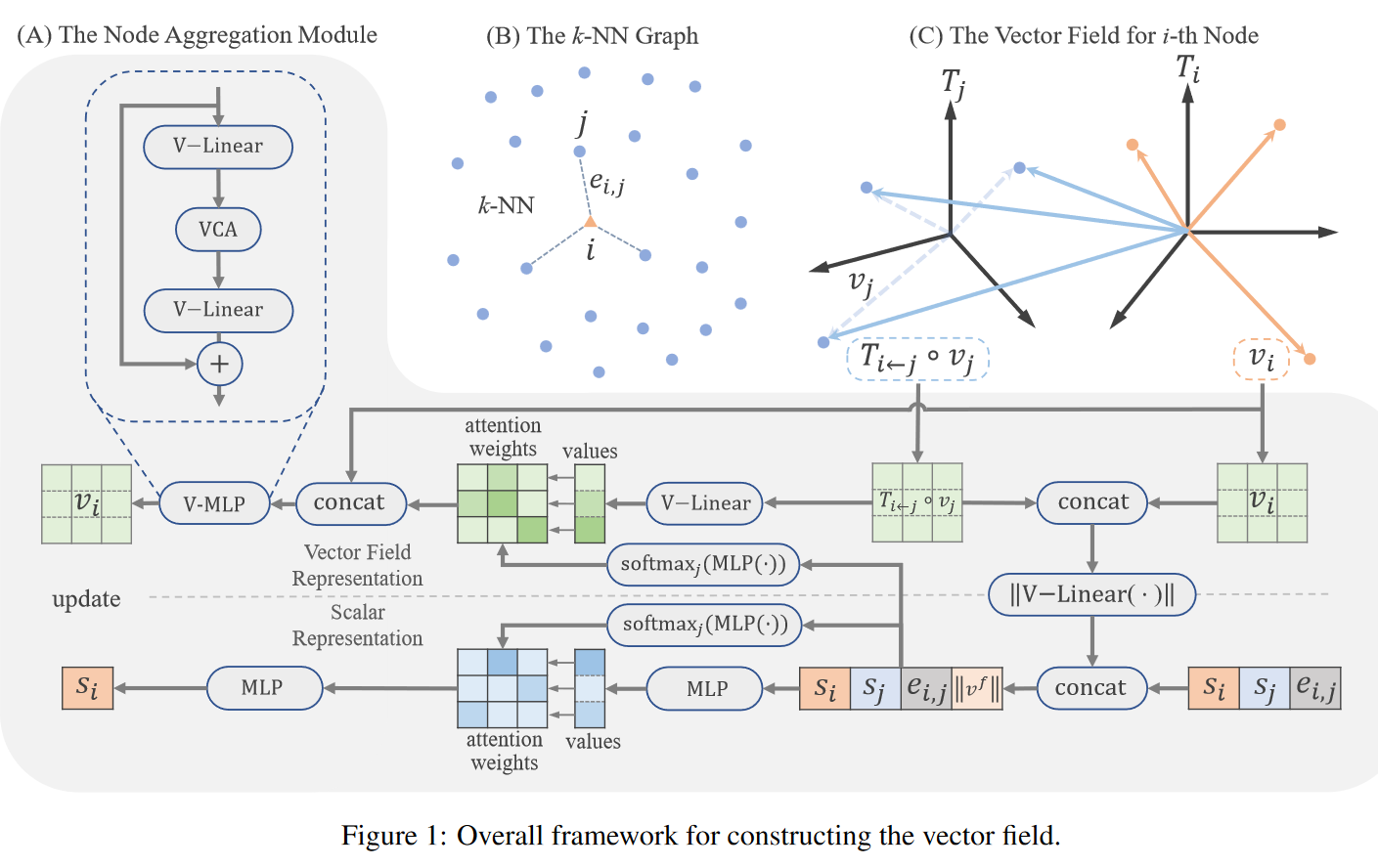
记号：

\(s_i\) 是点的scalar representation \(\in \mathbb{R}^d\)

\(e_{i,j}\)是边的标量特征  \(\in \mathbb{R}^d\)

\(v_i\) 是点的vector representation  很重要，是\(V\times 3\)矩阵, \(V\)  代表使用的向量数量

（\(d\) 和 \(V\) 是人为设定的, d=128,V=32（见4.1)

\(T_i\) 是每个氨基酸内部原子的局部坐标系

\(T_{i \to j}\) 是两个氨基酸间的变换矩阵,用于对不同点的 \(v_i\) 进行变换

• node aggregation
• edge aggregation
• global context

3.1 Initialization

正交化的细节:

• 以

  \(C_\alpha\)

  为原点，得到三个正交单位向量

• \(\beta_2=\alpha_2-\frac{(\beta_1,\alpha_2)}{(\beta_1,\beta_1)}\beta_1\)

  注意

  \(\beta_1\)

  单位向量,内积为1

• 最后还要记下来原点的坐标。T是一个list,包含基向量组成的矩阵R 和坐标原点

从Tj到Ti的变换矩阵是\(T_i^{-1}\circ T_j\)  （注意因为Ti不是绝对坐标，是相对坐标，所以这里除了线性变换之外，还有坐标原点的平移） 不是简单的矩阵相乘

文章为什么要使用vector representation，向量的方向有实际意义吗? 感觉vi和Ti坐标变换的结合是关键？

3.2

vector field

对于图中的每条边(i,j). 把两端点的特征\(v_i\)变换到同一个坐标系下然后concat，再过一个线性层得到\(v_{i,j}^f\)

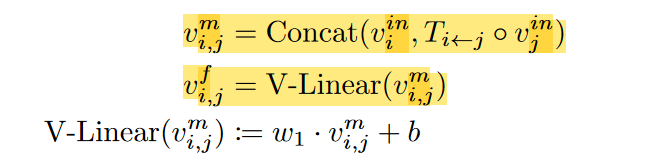
node aggregation

把vector field的模和标量特征concat,过MLP+softmax得到attention

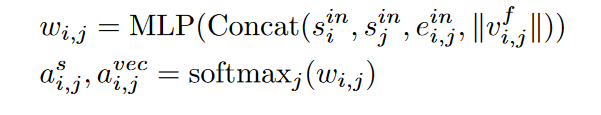
和attention对应相乘:把sij中的d个数分为H组,每组和aij中的一个head(是数)做数乘，最后再拼接起来

Comments