Skip to content

离散数学期末复习与历年卷题目

Sets

Definitions and Theorems

  • Functions

    • categories

      • one-to-one 单射,不能有两个变量对应函数值相同
      • onto满射
      • bijection

    • Growth of functions

    • Set Cardinality

    • Infinite sets: a set is infinite if and only if it has an infinite proper subset

    • Cardinality: \(f: A\to B\)
      • bijection \(|A|=|B|\)
      • one-to-one \(|A| \leq |B|\)
    • Countable infinite \(|A|=|Z^+|\)
      • \(Q^+\) is countable infinite: \(|Q^+|=|Z^+\times Z^+|\). \(n=1+2+\dots(p+q-2)+q\)
      • The union of countable number of countable sets is countable.
      • the set of finite subset of positive integers is countable: \(\{a_1,a_2\dots a_n\}\to 2^{a_1}+2^{a_2}+\dots 2^{a_n}\)
    • Uncountable infinite
      • \((0,1)\) is uncountable
        • Cantor Diagonal Argument \(x_i=0\) if \(d_{ii}\neq 0\), \(x_i=1\) if \(d_{ii}=0\)
      • The set of infinite subset of positive integers is uncountable. (use decimal representation)
      • the set of functions from \(\mathbb{Z}^+\) to \(\{1,2,3,4,5,6,7,8,9\}\) is uncountable (use decimal representation)
    • Schroder-Bernstein Theorem: \(|A|\leq |B|\) and \(|B|\leq |A|\), then \(|A|=|B|\)
    • Cantor's Theorem \(|S|<|\mathcal{P}(S)|\): construct \(B=\{x|x\in A \wedge x \notin f(x)\}\), proof that no \(f(s)=B\)

找集合恒等式的反例: 构造空集

(×）(2003 Fall) if \(A\times B\subseteq C\times D\), then \(A \subseteq C\) and \(B \subseteq D\)

反例: \(B=\emptyset\),\(A,C\)可以任意取,不需要是子集关系

Relations

Definitions and Theorems

  • Definition: a relation is a subset of \(A \times B\)
  • Properties
  • Equivalence Relations
    • Equivalence Relation 和Set partition 一一对应
  • Partial Ordering: reflexive,antisymmetric,transitive
    • Totally ordered set: every two elements of the poset is comparable (aka chain,linearly ordered set)
      • Well ordered set: \((S,\leq)\). \(\leq\) is a total ordering and every non empty subset of \(S\) has a least element. (every well-ordered set is a totally ordered set.)
    • Elements in a poset
      • Maximal:没有向上的边 Minimal:没有向下的边
      • Upper bound and Lower bound of set \(S\). \(\forall a \in S, l \geq a\)
      • lub and glb
    • Lattice: every pair of elements has a lub and glb
      • \((\mathbb{Z}^+,|)\), \((\mathcal{P}(S),\subseteq)\) is a lattice 用最大公约数/最小公倍数，交集/并集
      • every totally ordered set is a lattice
    • Topological Sorting: A total ordering \(\leq\) is compatible with the partial ordering \(R\): for all \(aRb\) , \(a \leq b\) (相当于把partial order 变成了total order)

(×）(2003) \((A,\leq)\) is a poset, if there is a unique maximal element of \(A\), then it is the greatest in \(A\)

反例: \(A\) 可以是一个无限集合,没有greatest. 但是可以分支出一个maximal

(2005) |A|=n,

  • reflexive: \(2^{n^2-n}\)
  • symmetric: \(\color{red}2^{(n^2-n)/2}\times 2^n=2^{(n(n+1)/2)}\) 注意对角线上可以是0或1
  • antisymmetric: \(\color{red}3^{n(n-1)/2}\times 2^n\) 对于矩阵非对角线上的一对对称的元素, 只能是(0,0),(0,1),(1,0). 对角线上可以是0或1
  • asymmetric \(3^{n(n-1)/2}\)，对角线上全为0

(1)How many relations are symmetric and antisymmetric? (2)How many total ordering relations on A

  • （1）矩阵非对角线的位置都是0,所以是\(2^n\)
  • （2）是一条链,\(n!\)

(2015) \(A=\{a,b,c\}\)(1)How many equivalence relations on A (2)How many partial order on A

(1) \(S(n,1)+S(n,2)+\dots +S(n,n)\)

\(\boxed{S\circ R=\{(a,c)|(a,b)\in R \wedge \color{red}(b,c)\in S\}}\) 对应矩阵\(M_R \times M_S\). S是放在后面的，类比函数复合‘

Graphs and Trees

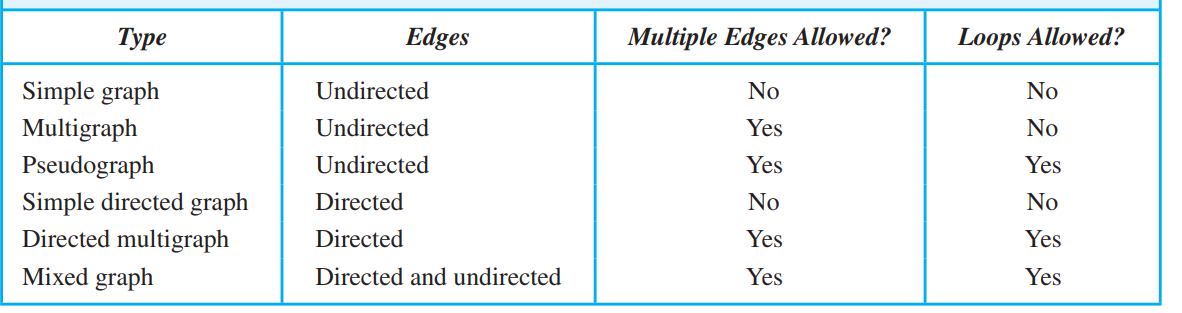
  • Basic concepts b80cc0b44ed1d3bd40fa7baac06dad43.png

  • Graph Isomorphism

  • Graph Connectivity

  • Bipartite Graph

  • Euler Graph

    • A connected multigraph has an Euler circuit if and only if each of its vertices has even degree.
    • A directed multigraph having no isolated vertices has an Euler circuit if and only if the graph is weakly connected and the in-degree and out-degree of each vertex are equal.

  • Hamilton Graph

    • (充分条件)Ore's Theorem: simple graph with \(n \geq 3\),\(\deg u+\deg v \geq n\), Hamilton circuit.
      • 如果是哈密顿路径,只需要\(\deg u+\deg v \geq n-1\) (添加一个虚拟节点,之后变成n+1个点的图,度数和\(\geq n+1\)
    • 必要条件
      • \(\forall S \subset V\), the number of connected components in \(\boxed{G-S}\) is \(\leq |S|\). (用于证明图没有哈密顿回路,尽量选割点割掉)

  • Planar Graph

    • Euler's Theorem: connected planar simple graph \(\boxed{r=e-v+2}\)
      • non-connected \(r=e-v+k+1\). k connected components
      • degree of regions \(\deg r_i\). \(\sum \deg r_i=2e\)
      • If G is a connected planar simple graph with \(v \geq 3\), then \(\boxed{e \leq 3v-6}\)
      • G has at least one vertex of degree not exceeding 5
      • If a connected planar simple graph has e edges and v vertices with v ≥ 3 and no circuits of length three, then \(e \leq 2v − 4\) (\(\deg r_i \geq 4\))
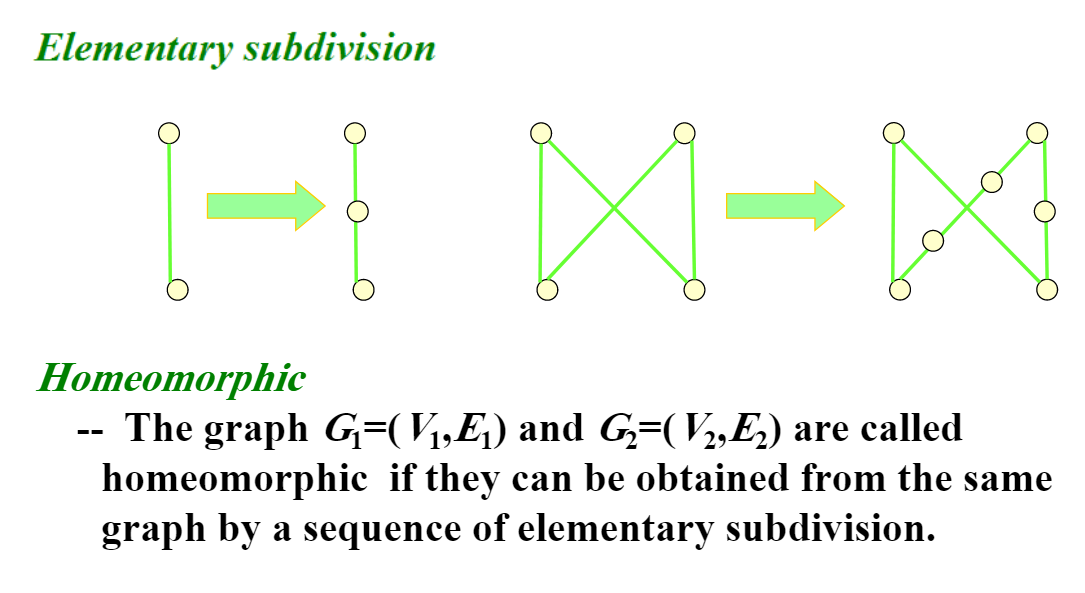
    • A graph is nonplanar if and only if it contains a subgraph homeomorphic to \(K_{3,3}\)or \(K_5\) 4ca907a7e91a5fa60a0b2d46a077d5df.png

  • Graph coloring

    • every planar graph is 4-colorable

  • Trees

    • full(every vertices have m children) m-ary tree \(n=mi+1\)
    • complete
    • balanced

Comments