静电场2

电势\(V=\frac{q}{4\pi\varepsilon_0 r}\) 注意电场强度是二次方，电势是一次方

无穷远处电势为0，P点点数电势\(V_P=\int_P^{\infty} Edx\)

\(\vec{E}=-\nabla V\) 负号，注意混合项的偏导

电容

\(C=\frac{Q}{U}=\frac{Q}{U_A-U_B}=\frac{Q}{\int Edl}\)

孤立球形导体,\(U=\frac{1}{4\pi \varepsilon_0}\frac{Q}{R},\boxed{C=4\pi \varepsilon_0R}\)

平行板 \(\boxed{E=\frac{\varepsilon_0 S}{d}}\), 有电介质就乘上\(\varepsilon\) 串并联注意\(d\)是否相等

平行柱面: \(E=\frac{\lambda}{2\pi \varepsilon_0 r}\)

\(U_A-U_B=\int_{R_A}^{R_B}Edr\) （注意积分上下限A,B和电压是反过来的

\(C=\frac{\lambda l}{U_A-U_B}=\frac{2\pi \varepsilon_0 l}{\ln (\frac{R_B}{R_A})}\)

电介质

电介质的极化

极化强度\(P=\frac{\sum \vec{p_e}}{V}\) 单位体积电偶极矩矢量和

介质\(P=x_e \varepsilon_0 E\)

表面束缚电荷密度\(\sigma'=P\cos\theta\), \(\theta\)是\(\vec{P}\)与平面法线夹角

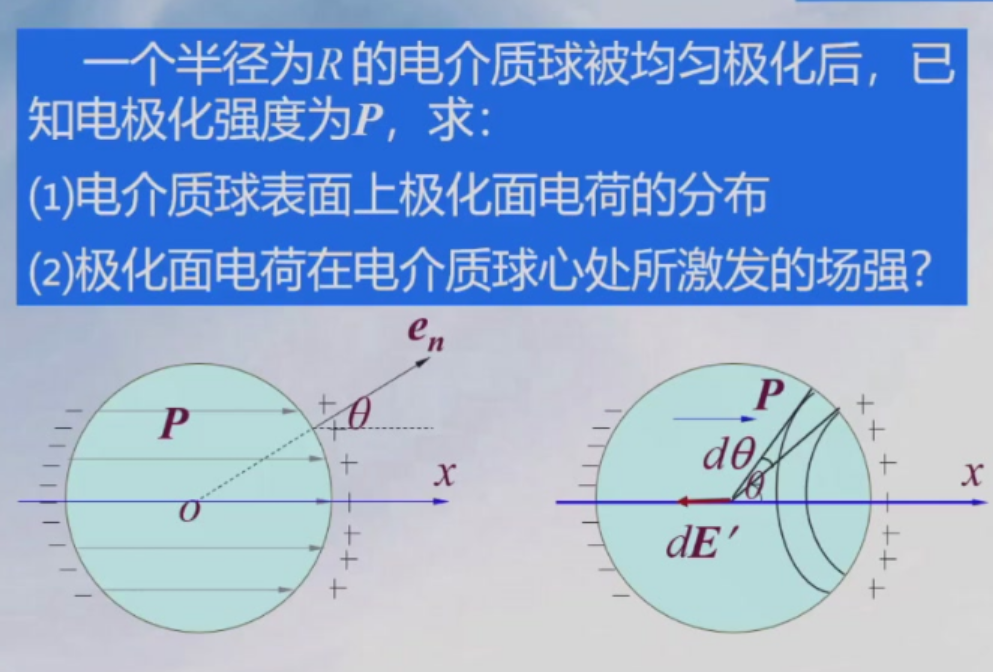
圆环,半径\(R\sin \theta\), 宽度\(Rd\theta\)

电介质中的场强

\(\vec{E}=\vec{E_0}+\vec{E'},E'\)为极化电荷激发的电场，方向与自由电荷激发的电场相反

\(E=\frac{\sigma_0}{\varepsilon_0}-\frac{\sigma'}{\varepsilon_0}\)

电位移矢量

定义\(\boxed{\vec{D}=\varepsilon_0\vec{E}+\vec{P}}\)

极化电荷面密度\(\sigma'=P\sin \theta\), 内表面\(-P\),外表面P

在各向同性介质中,将极化强度的定义代入\(D=(1+x_e)\varepsilon_0E=\varepsilon\varepsilon_0 E\)

\(\boxed{D=\varepsilon\varepsilon_0 E}\) \(\varepsilon\): 相对介电常数

有电介质的高斯定理

\[ \boxed{\oint \vec{D}\cdot d\vec{S}=q_0} \]

注意对介质来说,\(P\)和\(e_n\)方向相反。类似于前面电介质球最左侧的情况

注意第二类曲面积分符号，向内侧和外侧符号相反

\(D_1=D_2=\frac{\sigma}{\varepsilon_0}\) \(E=\)

静电场的环路定理(静电场是保守场，绕一圈回到原点，电势不变，做功为0）:

\[ \oint \vec{E}\cdot d \vec{l}=0 \]

如果用高斯定理解不出来，再加上环路定理列方程

例:两个电容器并联

电场的能量

电荷相互作用的静电能

\[ W=\frac{1}{2}\sum_{i=1}^n q_i U_i \]

\(U_i\)是其他电荷在\(q_i\)处产生的电势。积分形式

\[ W=\frac{1}{2}\iiint_V Udq \]

这里的\(V\)是对带电导体

电容器的静电能

已经带\(q\),增加电荷\(dq\), \(U=q/C\) \(dW=Udq\)

积分\(\int_0^Q \frac{qdq}{C}\)

\[ \boxed{W=\frac{1}{2}\frac{Q^2}{C}=\frac{1}{2}QU=\frac{1}{2}CU^2} \]

用能量法,\(F=-dW/dx\)

看成两个电容器并联\(C=C_1+C_2\)

静电场的能量

\(U=Ed,Q=\sigma S,E=\frac{\sigma}{\varepsilon \varepsilon_0}\)

代入得\(W=\frac{1}{2}\varepsilon\varepsilon_0 ESEd=\frac{1}{2}\varepsilon\varepsilon_0E^2 V\) \(V\)是电容器体积

定义电场能量密度\(w_e=\frac{W}{V}\)

\[ \boxed{w_e=\frac{1}{2}\varepsilon\varepsilon_0E^2=\frac{1}{2}ED} \]

对任何静电场\(w=1/2\vec{E}\cdot \vec{D}\)

\[ W=\frac{1}{2}\iiint_V \vec{E}\cdot \vec{D}dV \]

注意这里的\(V\)不是对带电导体，而是对整个空间积分

例: 均匀带电球壳产生电场的能量，球壳外真空

\(w_e=\frac{1}{2}\varepsilon_0 E^2\)

\(E=\begin{cases}0,r<R \\\frac{q}{4\pi \varepsilon_0 r^2} ,r>R\end{cases}\)

\[ W=\int_R^{\infty}w_e 4\pi r^2dr=\frac{q^2}{8\pi \varepsilon_0 R} \]

这里没说导体球, 是绝缘体，所以内部电场强度不为0

\(E=\begin{cases} \frac{qr}{4\pi \varepsilon_0 R^3} ,r<R \\\frac{q}{4\pi \varepsilon_0 r^2} ,r>R\end{cases}\)

分\((0,R)\)和\((R,+\infty)\)两段积分

计算均匀带电Q 导体球的静电能,球外为介电常数\(\varepsilon\)电介质

带电导体内部场强为0

内部\(D=E=0\)

外部\(D=\frac{Q}{4\pi r^2},E=\frac{Q}{4\pi r^2\varepsilon_0\varepsilon}(r>R)\)

\[ \int _{R}^{\infty} \frac{1}{2}DE\cdot \color{cyan}4\pi r^2dr=\frac{Q^2}{8\pi \varepsilon_0\varepsilon R^2} \]