Skip to content

11.Tree

Counting Trees

Counting nonisomorphic unrooted tree

  • 枚举最长链 （跟数异构体的思路有点像

etc.n=5: 3 trees

Counting nonisomorphic rooted tree

  • 在无根树的基础上选

Properties of Trees

  • internal vertices(have children)
  • leafs(no children)
  • m-ary trees: every internavertex at most m children
  • Full m-ary trees: every internal vertex m children
  • Complete m-ary trees: full m-ary tree that all leaves have the same level

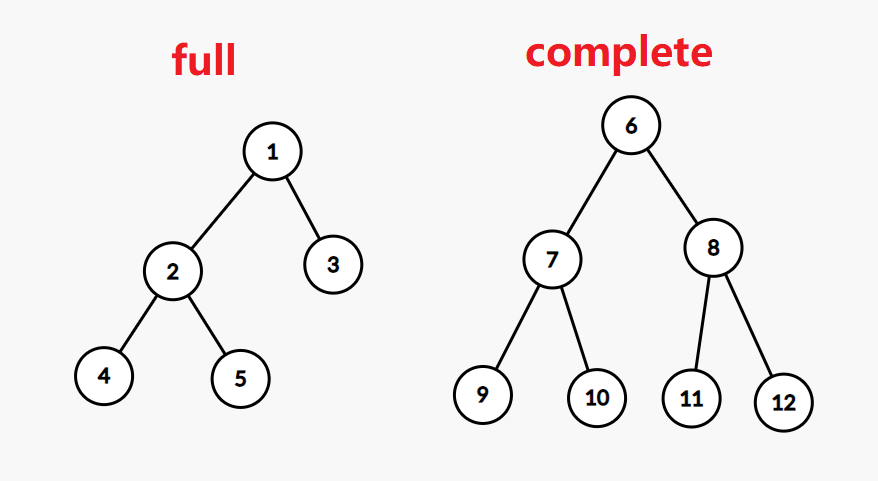
4663350c933d864958568db2987816ee.png

full m-ary trees只要求每个结点有m个或0个孩子,所以叶子可以在各种深度，比如哈夫曼树. 但是balance 必须在h或h-1

叶子数,节点数，深度计算

A full m-ary tree with i internal vertices contains \(\boxed{n=mi+1}\) vertices

Proof: 除了根,每个结点的父亲都是internal vertices

如果知道叶子数\(l\),就用\(\boxed{n=m(n-l)+1}\)找关系

  • Level: the length of paths from root to the vertex.(从0开始)
  • Height: maximum level(从0开始)
  • Balanced tree: all leaves are at levels \(\color{blue}h\) or \(\color{blue}h-1\)

There are at most \(m^h\) leaves in an m-ary tree of height h

Proof: 归纳. 高度h+1的树有最多m个高度h的子树

推论\(\boxed{h \geq \lceil \log_ml \rceil}\)

There are at least \(m^{h-1}\) leaves in a full and balanced m-ary tree of height h

因为balanced,所以h-1层往上一定是complete m-ary tree,有\(m^{h-1}\)个叶子节点. 往\(h\)层添加叶子时，每去掉h-1层的1个叶子，就会增加1个或2个叶子,所以叶子节点数量\(\geq m^{h-1}\)

推论:a full and balanced m-ary tree, \(h=\lceil \log_ml \rceil\)

Tree traversal

preorder traversal, inorder traversal, and postorder traversal 对应前、中、后序

reconstruct tree.

  1. 根据前序和每个结点儿子个数? 无法确定只有一个结点在左/右

prefix(Polish),infix,postfix(Inverse Polish) notation 注意infix必须有括号.

表达式求值: prefix 从后往前, postfix从前往后，将数字放到栈里，每遇到操作符就取出最上面两个 根据表达式画出树: 如果是postfix也是用栈的思路从前往后，自底向上建树

Spanning Tree

DFS/BFS

Mininum Spanning Tree:

  • Prim: 每次从与当前生成树T相邻的边里面选一条长度最小，且不成环的
  • Kruskal

binary search tree

Huffman Tree

Comments