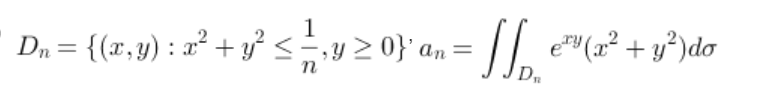Skip to content

2.1二重积分

二重积分

\[ \iint\limits_{\sigma} f(x,y) d\sigma \]

x型区域:

\[ \int_{x_1}^{x_2}dx\int_{y_1(x)}^{y_2(x)}f(x,y)dy \]

处理里面的积分时,把\(x\)看做常数,y是积分变量,最后的结果用x表示。

y型区域:

\[ \int_{y_1}^{y_2}dy\int_{x_1(y)}^{x_2(y)}f(x,y)dx \]

几何意义: 立体体积。积分区域\(\sigma\)是底面。

交换积分顺序及其应用

常见于处理\(e^{x^2}\)等原函数不初等的

\(\int_0^1te^{-t}dt=1-\frac{2}{e}\)

极坐标变换

\[ \int_{\alpha}^{\beta}d\theta\int_{r_1(\theta)}^{r_2(\theta)}f(r\cos \theta,r\sin \theta)\color{blue}{rdr} \]

如果点在区域内,\(\theta\)取0到\(2\pi\). \(r\)的下界取0

常见的区域边界:

  • 圆心在坐标轴上\(x^2+y^2=2ax\).化成\(r=a\cos \theta\)，范围\(0\leq r \leq a\cos \theta\)
  • 如果圆心在\((a,b)\), 令\(x=r\cos\theta+a,y=r\sin \theta+b\). \(d\sigma仍然=rd\theta dr\)

一般坐标变换

用到微分学中的Jacobi行列式(\(\color{red} 把x,y用u,v\))

\[\frac{\partial(x,y)}{\partial(u,v)}=\begin{vmatrix}\frac{\partial x}{\partial u}\ \frac{\partial x}{\partial v}\\ \frac{\partial y}{\partial u}\ \frac{\partial y}{\partial v}\end{vmatrix} \]
\[ \iint\limits_{\sigma} f(x,y) d\sigma=\iint\limits_{\sigma'} f(x(u,v),y(u,v))|\frac{\partial(x,y)}{\partial(u,v)}|dudv \]

对于极坐标变换\(x=r\cos\theta,y=r\sin\theta\). Jacobi行列式值为\(r\)

对于广义极坐标变换\(x=ar\cos\theta,y=br\sin\theta\). Jacobi行列式值为\(abr\)

其他的变换可通过求导或隐函数求导得到

例: 8ed6ca7ad426aed2a9a9c4708d2bb0c2.png

\(x=\frac{u}{\sqrt{n}},y=\frac{v}{\sqrt{n}},J=\frac{1}{n}\)

$$a_n=\iint \frac{1}{n2}e{\frac{uv}{n}}dudv(u2+v2)

$$

所以\(a_n \sim \frac{1}{n^2}(n \to \infin)\),因为\(e^{uv/n}\)趋近于\(e^0\),剩下部分的积分是\(\iint(u^2+v^2)dudv=\frac{\pi}{4}\)

Comments