3 Arithmetic
补充
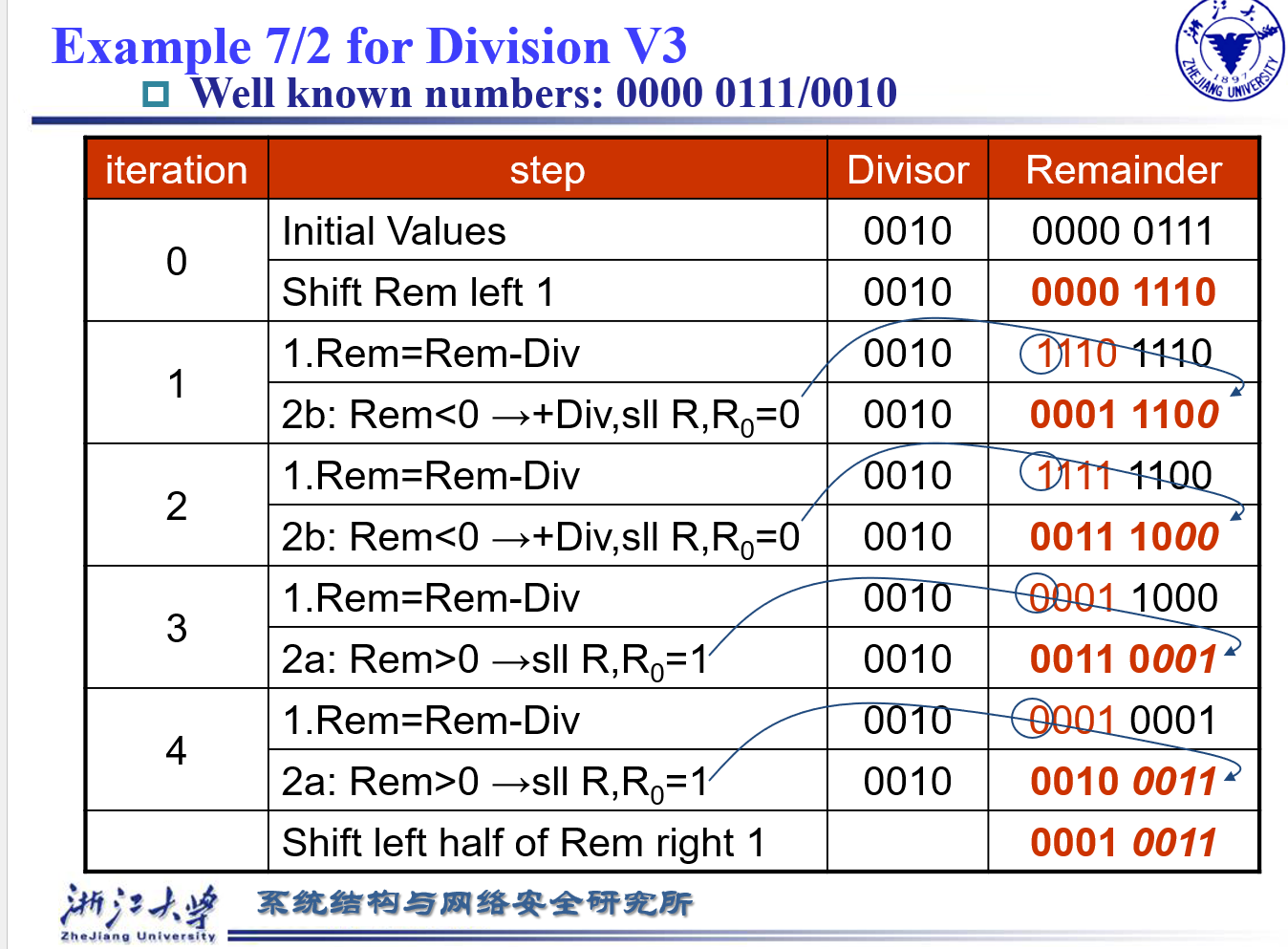
除法器
IEEE浮点数
浮点数定义
符号位S 指数 exp, 尾数fra 长度分别为\(E,F\)
bias一般是\(2^{E-1}-1\) (相当于excess \(2^{E-1}\)码)
| exp(\([0,2^E-1]\)) | fra | 表示的数 |
|---|---|---|
| 0 | 0 | 0 |
| 0 | ≠0 | 非规格化数 |
| \(1\sim2^{E}-2\) | \((-1)^S(1+fra)\cdot 2^{exp-bias}\) | |
| \(2^E-1\) | 0 | ±inf |
| \(2^E-1\) | ≠0 | NaN |
范围\([2^{1-bias},(2-2^{-F})2^{2^E-2-bias}]=[2^{-2^{E-1}+2},(2-2^{-F})2^{2^{E-1}-1}]\) 规律:上下界的指数的绝对值差1
精度 \(2^{-F}\)
| S | E | F | 范围 | 精度 | |
|---|---|---|---|---|---|
| 单精度(32) | 1 | 8 | 23 | \([2^{-126},(2-2^{-23})2^{127}]\) | |
| 双精度(64) | 1 | 11 | 52 | \([2^{-1022},(2-2^{-52})2^{1023}]\) | |
| 半精度(16) | 1 | 5 | 10 |
其他的浮点数: 注意尾数有没有hidden 1 指数是补码还是有bias
加法
- 把小指数对齐到大指数,尾数移位 (因为后面的位不重要)
- 尾数相加
- 规格化
- 舍入
乘法
- 指数相加,然后-bias
- 尾数相乘
- 规格化
舍入规则
guard/round/sticky- 一般的浮点数后面还会有 2 bits,分别称为 guard 和 round
- 只要 round 右边出现过非零位,就将 sticky 置 1,这一点可以用在加法的右移中,可以记住是否有 1 被移出,从而能够实现 "round to nearest even"。