2.Basic Structures
2.1 Definition of Set
Let S be a set. If there are exactly n distinct elements in \(S\) where n is a nonnegative integer, we say that S is a finite set and that n is the cardinality of \(S\) . \(|S|\)
Subset
Power set
\(\mathcal{P}(S)=\{x|x \subseteq S\}\)
- \(x \in P(S) \to x \subseteq S\)
- \(x \in S \to \{x\} \subseteq S\)
- \(|S|=n \to |\mathcal{P}(S)|=2^n\)
\(\mathcal{P}(\emptyset)=\{\emptyset\}\)
\(\mathcal{P}(\{\emptyset\})=\{\emptyset,\{\emptyset\}\}\)
Prove theorems of power sets.
\(A\subseteq B \leftrightarrow P(A)\subseteq P(B)\).
Proof: the subset of \(A\) is also subset of B, so \(P(A)\subseteq P(B)\). if \(P(A) \subseteq P(B)\) ,because \(A \in P(A)\) (by definition), then \(A \in P(B)\)(properties of subset),then \(A \subseteq B\)(by definition of subset)
\(A=B \leftrightarrow P(A)=P(B)\).
\(P(A) \in P(B)\to A \in B\)
注意用这两条定义进行\(\in\) 和\(\subseteq\)之间的转换
2.2 Set Operations
symmetric difference \((A\cup B)-(A\cap B)\)
Identity
\((A-B)=A\cap\bar{B}\)
\(A \cap (A \cup B)=A\). 对应之前的absorption\(p \wedge(p \vee q)=p\), 用集合的语言看更显然


Cartesian Product
可以用二维坐标系的方法表示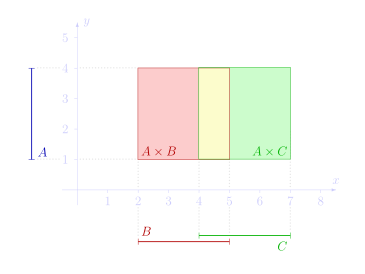
2.3 Functions
\(f:A \to B\)
Domain: \(A\) Preimage:\(a\)
Codomain: \(B\). Image:\(b\)
Range of \(f\)( \(\{f(x)|x\in A\}\))
\(f(S)=\{f(x)|x \in S\}(S \subseteq A)\)
\(f(A \cup B)=f(A)\cup f(B)\) Proof: 注意证明集合相等的方法
 \(f(A \cap B)\subseteq f(A) \cap f(B)\)
\(f(A \cap B)\subseteq f(A) \cap f(B)\)
etc .\(f(x)=x^2(x \in \mathbb{R}),A=\{x \leq 0\},B=\{x \geq 0\}\)
The Graph of Functions \(\{(a,b)|a \in A \wedge f(a)=b\}\)
Classification of Functions
- One-to-One(injective) \(\forall a\forall b(f(a)=f(b)\to a=b)\)
- Onto(surjective) \(\forall b \in B\existssss a \in A(f(a)=b)\)
- Both one to one and onto(bijective/one-to-one correspondence) If bijective, then A and B have same cardinality
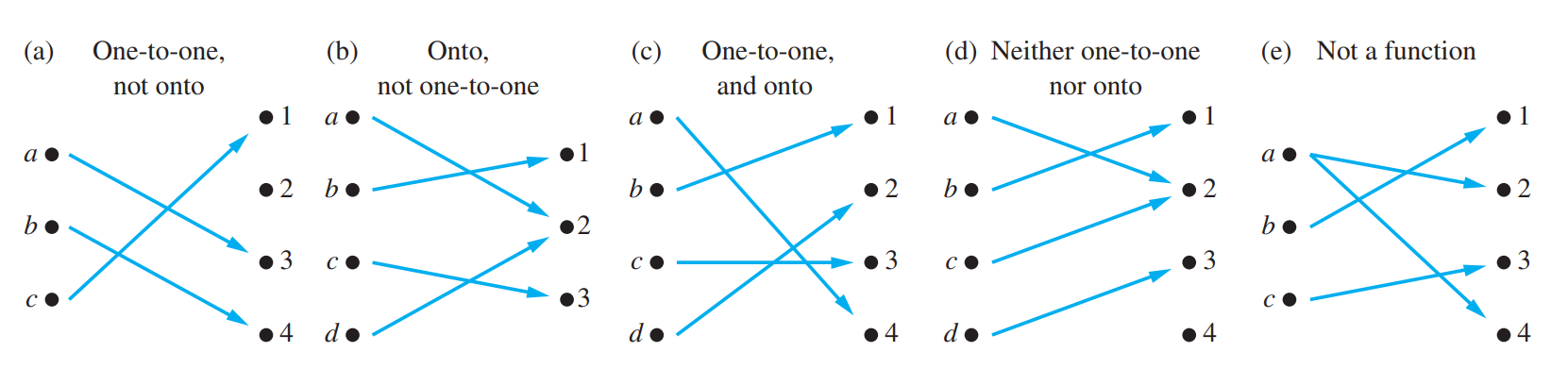 Inverse Function: requires bijection
Inverse Function: requires bijection
\(f(x)=\frac{x+1}{x+2}\) bijection,but not \(\mathbb R\) to \(\mathbb R\) ### Special Functions
\([x]\)
证明性质的方法: \(x=n+\varepsilon\)
Cardinality of Infinite Sets
Definition of cardinality
if and only if \(f:A \to B\). \(f\) is a bijection, then \(|A|=|B|\)
if \(f: A \to B\), \(f\) is an injection, then \(|A| \leq |B|\)
If \(|A| \leq |B|\) and \(|A| \neq |B|\). then \(|A|<|B|\)
Example: prove \(|(a,b)|\)=\(|(0,1)|\)
\(f(x)=a+(b-a)x\) is bijective
\(A\subset B\), then \(|A|\leq |B|\)
可以取等,比如偶数和正整数
Countable Sets
A set that is either finite or has the same cardinality as the set of positive integers called countable. When an infinite set \(S\) is countable, we denote the cardinality of \(S\) by \(\aleph_0\) ( aleph null \()\). If \(|A|=\left|\mathbb{Z}^{+}\right|\), the set \(A\) is countable infinite.
Example: prove \(\mathbb{Z}\) is countable
Try to rearrange the elements in a sequence. For example 0,1,-1,2,-2,3,-3...
\(f(n)=\begin{cases}\frac{n}{2},n =2k \\ -(n-1)/2,n=2k+1\\\end{cases}\)
Cantor Table
Example: prove \(\mathbb{Q}^+\) is countable
Let \(r=\frac{p}{q} \in\mathbb{Q^+},p,q \in \mathbb{Z}^+\). \(S=\{(p,q)\}=\mathbb{Z}^+ \times \mathbb{Z}^+, f(r)=(p,q)\)
Then \(f: \mathbb{Q}^+ \to S\) is one to one.
so \(|\mathbb{Q}^+| \leq |S|\)
Because \(\mathbb{Z^+}\subset \mathbb{Q}^+\), so \(|\mathbb{Z^+}|\leq |\mathbb{Q}^+|\)
We only need to prove \(|S|=|\mathbb{Z}^+|\)(aka \(Z^+ \times Z^+\) is countable)

For every pair (p,q), \(n=\frac{(p+q-2)(p+q-1)}{2}+q\) is a bijection. so \(|S|=|\mathbb{Z}^+|\)
Show that the set of the real numbers with decimal representations consisting of all 1s is countable
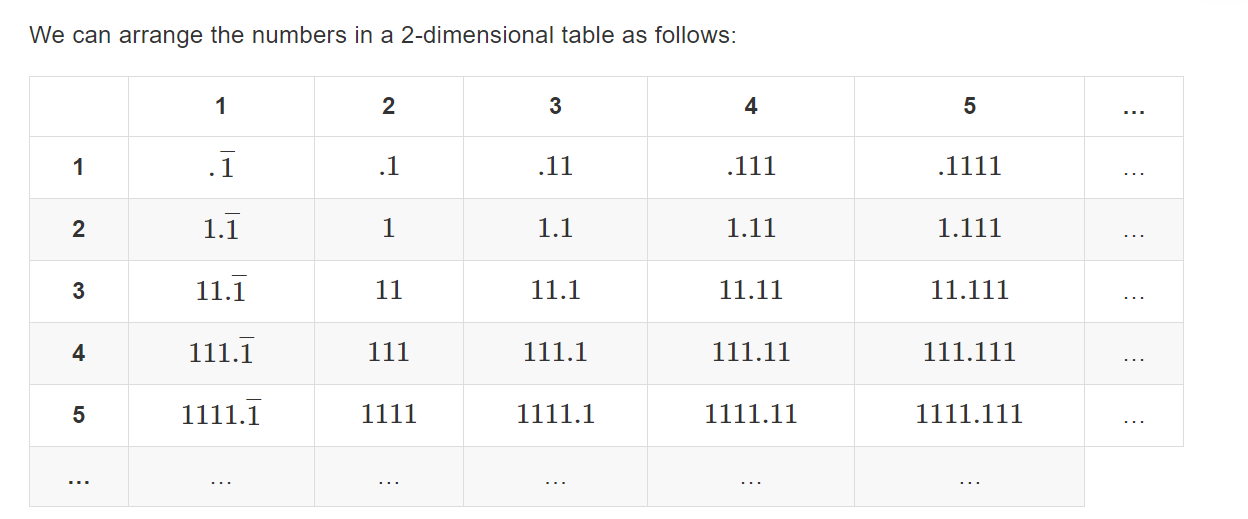 每一行的整数部分相同。每一列的小数部分相同(除了第一行,因为没有.0所以错开了)
每一行的整数部分相同。每一列的小数部分相同(除了第一行,因为没有.0所以错开了)
Properties of Countable Sets
- No infinite set has a smaller cardinality than a countable set
- The union of two countable sets is countable.
- The union of countable numbers of countable sets is countable. For example, \(Z^+\times Z^+\) is countable
Proof:
-
Suppose that\(|A|<|Z^+|\) , \(f:A \to Z^+\) is one-to-one.Because the range of \(f\) must be infinite. \(\forall n \in Z^+\), we can always find the \(n^{\text{th}}\) smallest element \(m\) in the range of \(f\). Because \(f\) is one-to-one, there exist a unique \(x\) that \(f(x)=m\) . so \(g(n)=x\) is a bijection. \(|A|=|Z^+|\), contradiction!.
-
List the elements as \(a_1,b_1,a_2,b_2\dots\)
-
\(A_i=\{a_{i1},a_{i2}\dots\}\) . List the elements as \(a_{11},a_{12},a_{21},a_{13},a_{22},a_{31}\)
Cantor Diagonalization Argument.
Construct an object that is not a member of countable set. 用于证明集合不可数
The set of real numbers in \((0,1)\) is uncountable
\(f: \mathbb{Z}^+ \to A=\frac{1}{n+1}\) is one-to-one, so \(|\mathbb{Z}^+| \leq |A|\). We need to prove \(|\mathbb{Z}^+| \neq |A|\)
Assume \(A\) is countable, then let \(A=\left\{r_1,r_2\dots r_n\right\}\) Represent each real number in the list using its decimal expansion. e.g., \(1 / 3=.3333333 \ldots . . . . ., 1 / 2=.5000000 \ldots . . . . \text{but not }0.4999999 . . . \ldots .\).
Now construct the number \(x=0 . x_1 x_2 x_3 x_4 x_5 x_6 x_7 \ldots\)
Then \(x\) is not equal to any number in the list.(Because it has at least one digit different from \(r_i\). For example, for \(r_1\), \(x_1 \neq d_{11}\)) Hence, no such list can exist and hence the interval \((0,1)\) is uncountable
Example. Show that the set of the real numbers with decimal representations consisting of all 1s or 9s is uncountable(all 1s or 9s是指由1和9组成,如0.1919。不只是全1或全9)
\(x_i=\begin{cases} 1,d_{ii}=9 \\ 9,d_{ii}=1 \text{\ or }d_{ii} \text{does not exist} \end{cases}\)
Schroder-Bernstein Theorem
Schroder-Bernstein Theorem: \(|A| \leq |B|\) and \(|B| \leq |A|\), then \(|A|=|B|\).
Only need to find two one-to-one functions.
Example 1: \(|(0,1)|=|\mathbb{R}|\)
Method 1: \(f(x)=\tan x(|x| \leq \pi/2)\) is bijection \(|(-\pi/2,\pi/2)|=|\mathbb{R}|\). and \(|(a,b)|=|(0,1)|\)
Method 2: Use Schroder-Bernstein Theorem: \(f(x)=x((0,1)\to \mathbb{R})\) is one to one. \(f(x)=\frac{1}{1+e^{-x}}(\mathbb{R}\to (0,1))\) is one-to one.
Example 2: \(|[0,1]|=|\mathbb{R}|\)
We can also use\(f(x)=x\) and \(f(x)=\frac{1}{1+e^{-x}}\) . because \(f\) is not required to be onto.
Example 3: \(|[0,1]|=|(0,1)|\)
\(f(x)=\frac{1}{3}+\frac{1}{3}x\) from \([0,1]\to [1/3,2/3]\).
Example 4: The set of infinite subset of positive integers is uncountable.
aka. \(|\mathcal{P}(\mathbb{Z}^+)|=|\mathbb{R}|\)
\(S\in \mathcal{P}(\mathbb{Z^+})\). \(d_i=\begin{cases}0,i \notin S \\ 1,i \in S \end{cases}\) \(f(S)=0.d_1d_2\dots d_n \in (0,1)\)
For \(x \in (0,1)\), use the binary expansion \(x=0.d_1d_2\dots d_n\).(use 0.110000...instead of 0.1011111..)
Then by Schroder-Bernstein Theorem, \(|\mathcal{P}(\mathbb{Z}^+)|=|(0,1)|=|\mathbb{R}|\)
However,the set of finite subset of positive integers is countable
\(\{a_1,a_2\dots a_n\}\to 2^{a_1}+2^{a_2}+\dots 2^{a_n}\) (because the set is finite,the integer exists)
This function(\(S\to Z^+\)) is one-to-one and onto.(onto because base 2,use binary expansion of every integer). So \(|S|=|Z^+|\)
Cantor's Theorem
Cantor's Theorem: \(|S|< |\mathcal{P}(S)|\)
Proof: \(f(x)=\{x\}\) is one to one. so \(|S| \leq |\mathcal{P}(S)|\). We only need to prove that \(|S|\neq |\mathcal{P}(S)|\). For all \(f:S \to \mathcal{P}(S)\) , \(f\) is not onto.
Let \(\boxed{B=\{x \in A|x \notin f(x)\}}\). It is obvious that\(B \subseteq S,B \in \mathcal{P}(S)\).
For every \(s\in A\).
- If \(s\in B\), then by definition of \(B\), \(s\notin f(s)\). so \(B \neq f(s)\). (Noted that this construction is similar to \(x_i=3(d_{ii}\neq 3),x_i=2(d_{ii}=3)\) in Cantor Diagonalization Argument)
- If \(s \notin B\), then \(s \in f(s)\). so \(B\neq f(s)\)
Because we can't find \(s\) that \(f(s)=B\). so \(f\) is not onto. Q.E.D.
The Continuum Hypothesis(连续统假设)
from Example 4:\(|\mathcal{P}(\mathbb{Z}^+)|=|\mathbb{R}|\). 记\(|\mathbb{R}|=c\),则\(2^{\aleph_0}=c\). 而连续统假设认为\(\aleph_0\)和\(c\)之间没有其他的基数, 即\(\aleph_1=c\),或\(2^{\aleph_0}=\aleph\)
Applications
Show that the set of functions from \(\mathbb{Z}^+\) to \(\{1,2,3,4,5,6,7,8,9\}\) is uncountable
Hint: prove \(|S|=|(0,1)|\)
\(x=0. d_1 d_2\dots d_n\). we associate a function \(f\) to \(x\) such that \(f(n)=d_n(n=1,2,3\dots)\). (小数的每一位确定\(f\)的一个取值,不同的实数对应的函数不同). (A few functions are left out, because of forbidding representations such as 0.239999 . . ..).
This is a bijection from \((0,1)\) to a subset of \(S\). so \(|S| \geq |(0,1)|\), uncountable.
Show that the set of finite strings S over a finite alphabet A is countably infinite
Assume an alphabetical ordering of symbols in A. Show that the strings can be listed in a sequence. First list
- All the strings of length 0 in alphabetical order.
- Then all the strings of length 1 in lexicographic (as in a dictionary) order.
- Then all the strings of length 2 in lexicographic order.
- And so on.
As the set of functions is uncountable while the set of finite strings(computer programs) is countable. So not all functions are computable. 这是计算理论的一个结论
References: