Skip to content

期末复习

历年卷总结+期末复习

期末复习

  • https://note.isshikih.top/cour_note/D2CX_AdvancedDataStructure/
  • https://zhoutimemachine.github.io/note/courses/ads-final-review/
  • https://zhoutimemachine.github.io/note/courses/ads-hw-review/
  • https://yaoyaolingbro.github.io/notebook/ZJU_CS/ADS/
  • 历年卷
  • https://file.cc98.org/v2-upload/ycpptj50.pdf
  • https://pan.baidu.com/s/1rpEiPt-vqOw3Ys0FagH6qA qwhj
  • https://www.yuque.com/xianyuxuan/coding/ads_exam_1#ilZRY

势能分析法

AVL& Splay

AVL

性质:

  • 树高严格\(O(\log n)\)

插入一个点后，可能会破坏关系。称插入的点为Trouble maker，递归向上找到的第一个不满足关系的点为trouble finder. (手动模拟的时候，最好把h写出来，以免找错,finder可能在上层

LL Rotation: 1次旋转，把B换到A的位置

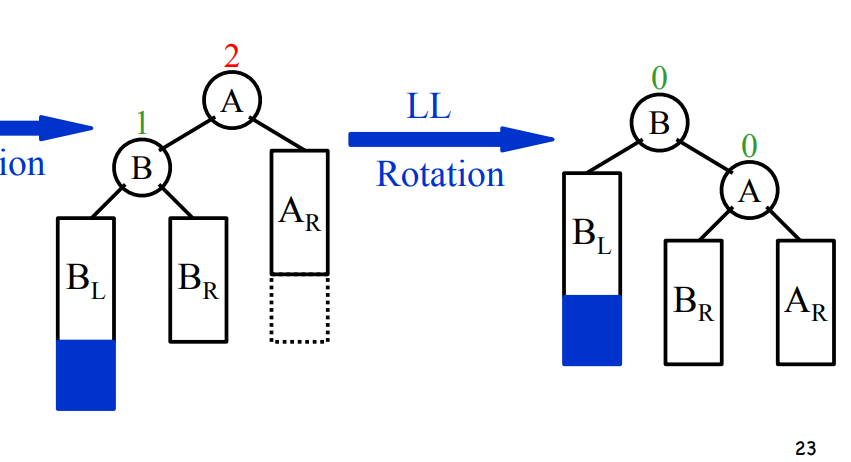
image.png

trouble finder是A, 插入点在B的左儿子子树中（也有可能是那个点)

LR Rotation:2次旋转，CB互换，CA互换

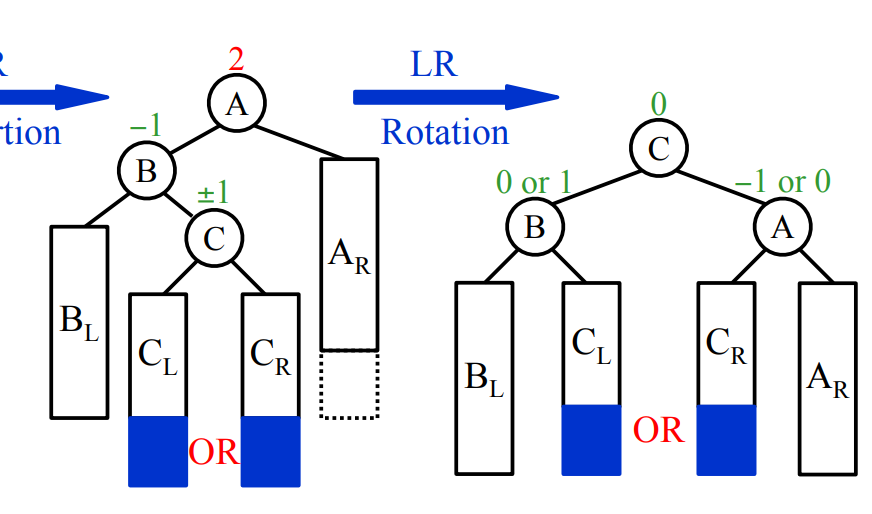
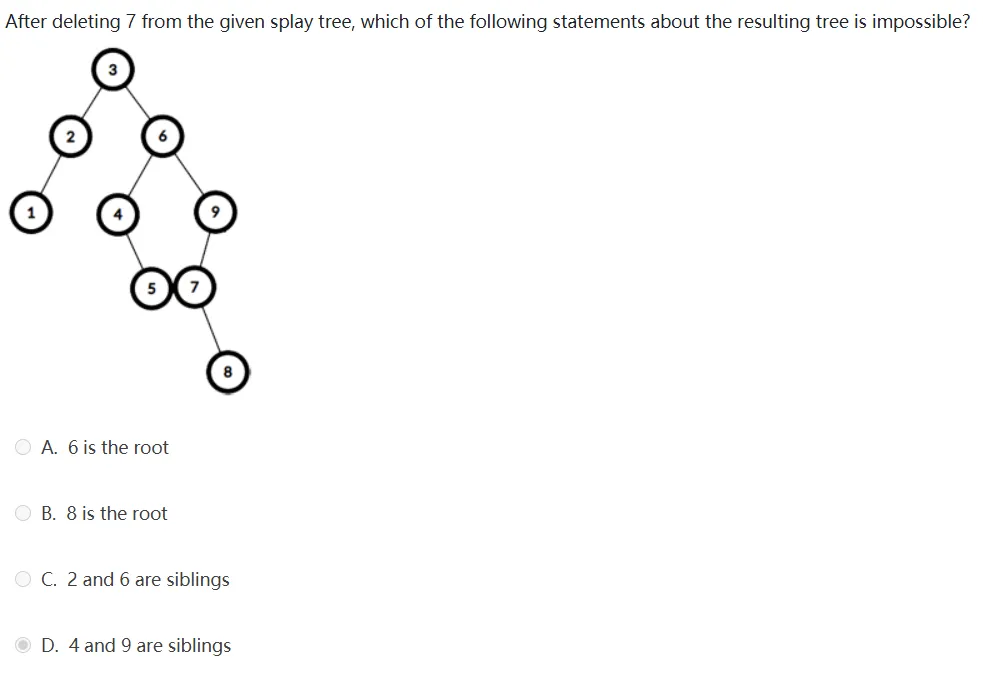
image.png

Splay的删除: 把x转到根后删除，得到l,r两个子树

  • 找到l中的最大值并转到l的根，把右子树r接过去
  • 或者找到r中的最小值，左子树l接过去

image.png

(F) In an AVL tree, it is impossible to have the balance factor of every non-leaf node to be +1.

2个节点的树

红黑树&B+树

红黑树

性质:

  • 根节点是黑色的(如果插入Case1染红父节点，如果父节点是根，最后还要染黑)
  • 红色节点两个儿子都是黑色的
  • 根节点到NIL节点长度相同。

推论:

  • 红节点不可能只有一个非NIL的孩子

插入: 插入节点是红色的。父亲是红色时进行双红修正。两个节点的时候一红一黑。3个节点可能触发Case3

  • Case1只需要重新染色，但会把旋转向上传递
  • Case2旋转，转化为Case3
  • Case3重新染色第二层，然后旋转

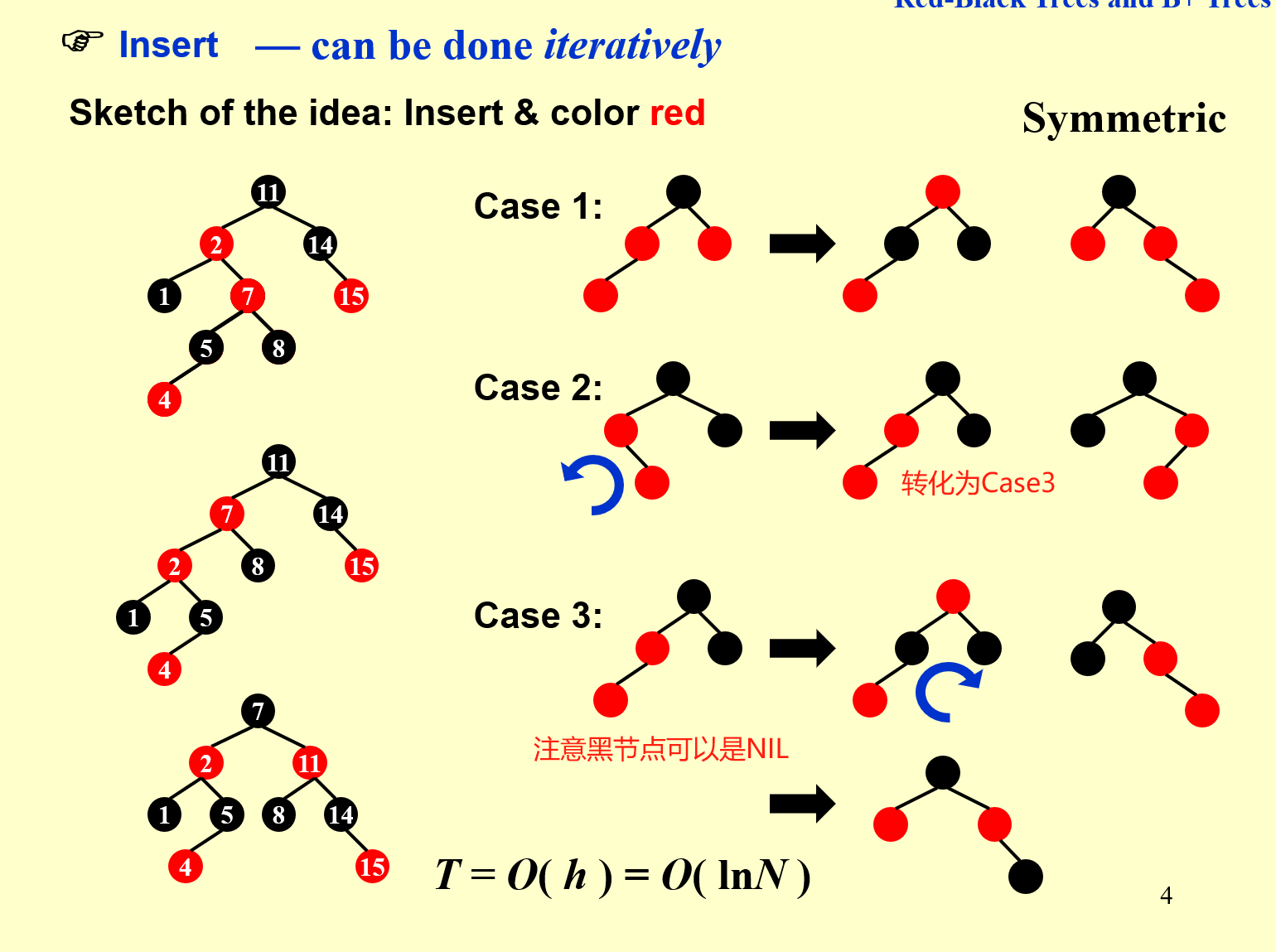
image-20240623185115384

BST的删除:删除BST树中的某一个几点，会有以下3种情况：

  • 待删除节点没有孩子。直接将其父节点的地址域置空即可 待删除节点有一个孩子。对于第二种情况，因为其只有一个孩子，删除节点后直接将其孩子的地址写于父节点相应的地址域即可 待删除节点有两个孩子。如果直接删除，你无法知道将其两个孩子节点如何安置，所以此处不能直接删除，此处可以使用待删除节点的前驱节点或者后继节点(前驱和后继节点下文具体描述)的值直接将待删除节点的值覆盖掉，然后再删除其前驱节点或者后继节点即可，根据前驱节点和后继节点的特性，就可将问题转换为第一种或者第二种情况。

前驱节点：当前节点左子树中值最大的节点(左子树的最右节点)。 后继节点：当前节点右子树中值最小的节点(右子树的最左节点)。 只有一个孩子或者没有孩子。

B+树

All nonleaf nodes (except the root) have between⌈M/2⌉ and M children.

Inverted File Index

  • stemming 留下词干

  • stop words 频率太高的词

  • ranked retrievalimage.png

左偏树&斜堆

右路径的代价估计：

heaps

A leftist heap with the null path length of the root being r must have at least \(2^{r+1}−1\) nodes.

贪心

activity selection: 我们只需要按照结束时间从小到大排序，遍历这些区间，能塞下就塞

哈夫曼树： 每个节点要么两个子节点，要么没有子节点

分治

Closest Points

平面上最近点对

  1. 将点对分为左右两部分，分别求解最近点对；
  2. 寻找跨越分界线的点对，从中寻找最近点对；
  3. 比较三者的大小，取最小值

\(O(n\log n)\)

image-20240623131356153

主定理

image-20240623135116196

展开\(T(n)=n^{(2^k-1)/2^k}T(n^{1/2^k})+O(n^{(2^k-1)/2^k}\log n)\)

搜索

n皇后问题

n*n棋盘 要求不能在一条横线，竖线，斜线上

image-20240622223912791

这题是找X任意下能赢的方案数（就当对手死机了)，左上到右下着，竖着，横着3种方式

In the 4-queens problem, (x1, x2, x3, x4) correspond to the 4 queens' column indices. During backtracking, (1, 4, 2, ?) will be checked before (2, 4, 1, ?), and none of them has any solution in their branches.

(2,4,1,3)可以

Turnpike

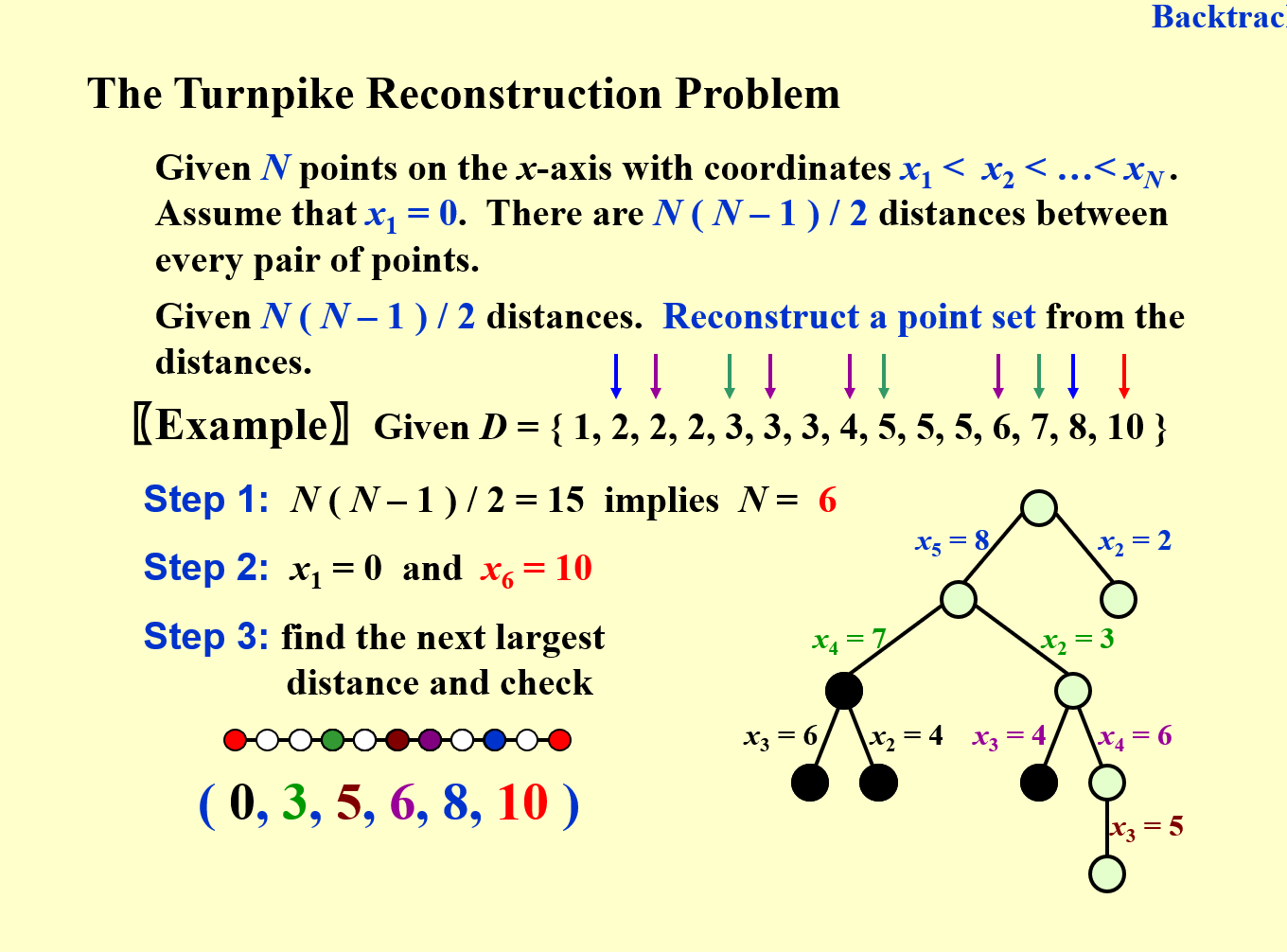
image-20240623132825102

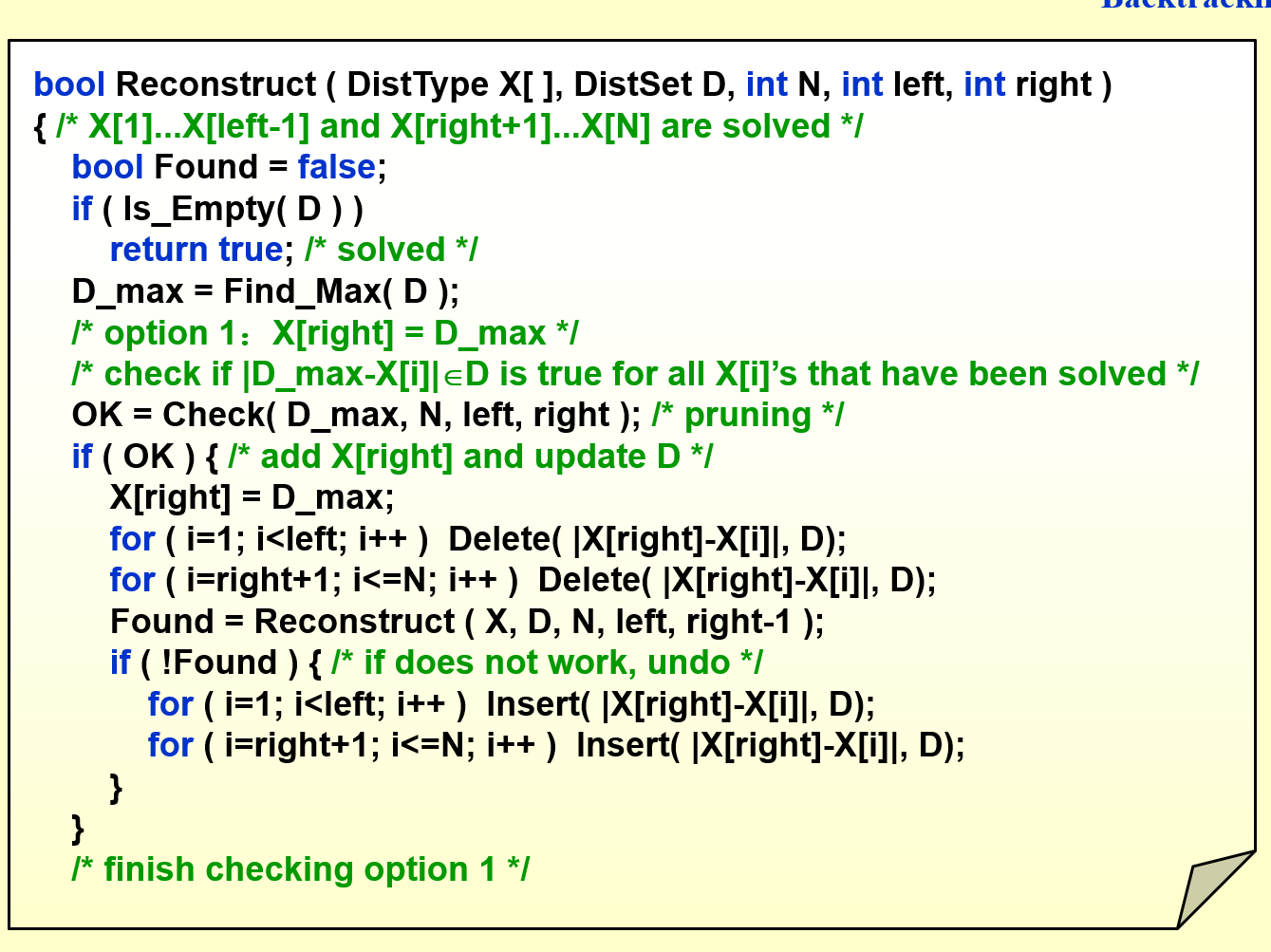
image-20240623132856524

每次选一个最大的距离作为x[i], 然后check

image-20240623113424738

alpha-beta

NP Completeness

NP: Nondeteministic Polynomial

  • All NP problems can be solved in polynomial time in a non-deterministic machine
  • 可以在多项式时间内判定

img

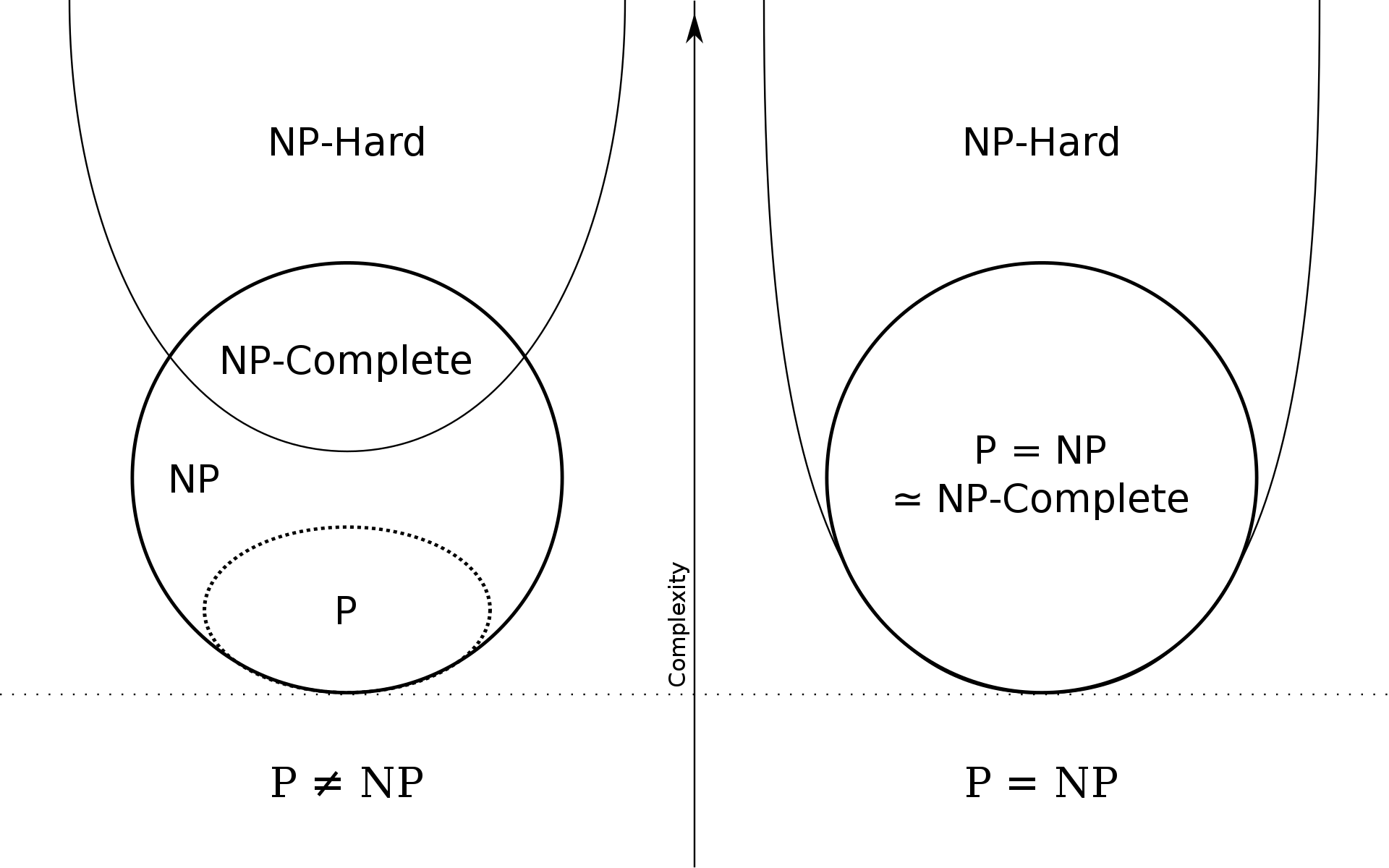
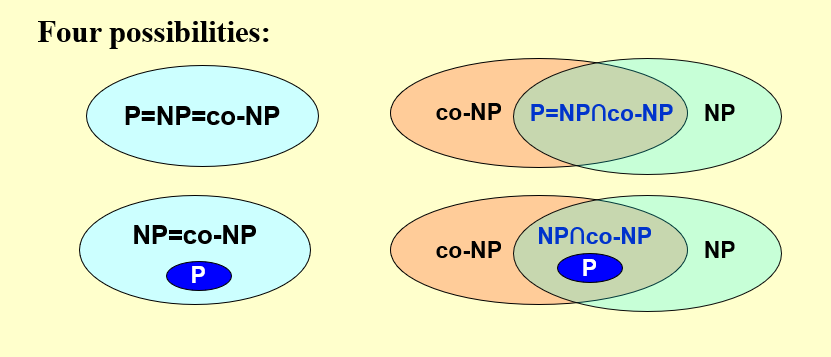
注意:NPC是NP与NP-Hard的交集

属于NP的问题

  • 找一个哈密顿回路(可以O(n)判定)
  • TSP: 给出图G和常数K，判断是否有一个哈密顿回路，总长度<=K
  • Vertex Cover
  • satisfiability

不是NP的问题:

  • 判定一个图不存在哈密顿回路
  • 停机问题（不可判定）

L1规约到L2 \(\boxed{L_1 \leq_P L_2}\) (注意不等号方向,大于号那边是被规约)

01背包的判定是NPC, 01背包是NP-HARD

image-20240623203728463

近似算法

装箱问题

给定N个大小为[0,1]的item，一个 bin 的大小为 1，尝试寻找最少的能够装载所有 item 的 bin 的数量

  • Online

    • next fit (上一个能放就放) 近似比2 (不会连续2个bin<0.5)
    • first fit (在当前所有桶里找第一个能放的放）近似比1.7 (最多一个bin<0.5)
    • best fit(找能放的中剩余空间最小的放) 1.7
    • online 理论最优近似比\(\frac{5}{3}\)

  • offline: item按照size 降序排序 , 然后使用next fit或first fit 使用不超过\(\boxed{\frac{11}{9}M+\frac{6}{9}}\) 其中\(M\)为精确解

image-20240623194514882

背包问题

容量和利润都是实数。贪心做法按\(\frac{p_i}{w_i}\)排序或按最大\(p_i\)，两种做法取最优，近似比2

DP做法是\(O(nV)\) 但是\(V\)是权值可以很大 所以是伪多项式算法

选取一个\(k\), 设$v_i'=\lfloor v_i/k\rfloor $ 对\(v_i'\)做背包，复杂度\(O(nV/k)\)

近似比:

\(SOL/OPT\geq 1-\varepsilon\) 近似比\(\alpha=\frac{1}{1-\varepsilon}=1+\frac{\varepsilon}{1-\varepsilon}\)

设\(k=\frac{\varepsilon v_{\max}}{n},V\leq nv_{\max}\) 复杂度为\(\boxed{O(\frac{n^3}{\varepsilon})}\)

可以根据需要的近似比，选择合适的k，越近似于最优解，复杂度越高。

近似比为\(1+\varepsilon\). 复杂度\(O(f(n,\varepsilon))\)

  • 如果\(f\)是n的多项式，称为PTAS 如\(n^{2/\varepsilon}\)
  • \(f\)是\(n,1/\varepsilon\)的多项式，称为FPTAS 完全多项式时间近似范式

背包是FPTAS. 设\(\varepsilon*=\frac{\varepsilon}{1-\varepsilon}\) 代入得复杂度为\(O(n^3(1+\frac{1}{\varepsilon*})^3)\)

image-20240623143932139

Hopfield NN

定义:给出边\(G(V,E,W)\), 每个点状态\(s_v\in\{-1,1\}\),边权有正负。\(w(u,v)>0\) 代表u,v状态不同，反之则相同。称\(\boxed{w_es_us_v<0}\)的为good edge。求一个分配方案，使得每个点都满足\(\sum_{v\in E(u)} w_es_us_v\leq 0\)

算法: 先随机设置状态。每次迭代找到所有不满足条件的点，将其取反。

定理: 最多在\(\boxed{\sum_e |w_e|}\)次迭代后找到解！

证明: \(\Phi=\sum \text{good edge的边权绝对值}\) 翻转不满足条件的点, \(\Phi\)增加

最大割

相当于把所有边都设为\(w_{uv}>0\) 如果是割中的边，则u,v种类不同 \(w_e u_ev_e <0\) ，就是好边

因此修改HopfieldNN的目标函数，最大化好边的边权和

所以 \(\sum_{(u,v)\in A} w_{uv}\leq \frac{1}{2}w(A,B)\) 对于B同理，代入最上面的不等式 得 $$ w(A,B)\leq 2w(A,B) $$

There exists a 2-approximation algorithm for max-cut 其中\(w(A*,B*)\)代表全局最优解

近似范式 每次增加\(\frac{2\varepsilon}{|V|}w(A,B) \to(2+\varepsilon)w(A,B)\geq w(A*,B*)\)： \(O(n/\varepsilon\log W)\)

image-20240513152526506

每迭代\(n/\varepsilon\) 次, 增加了\(2w(A,B)\)

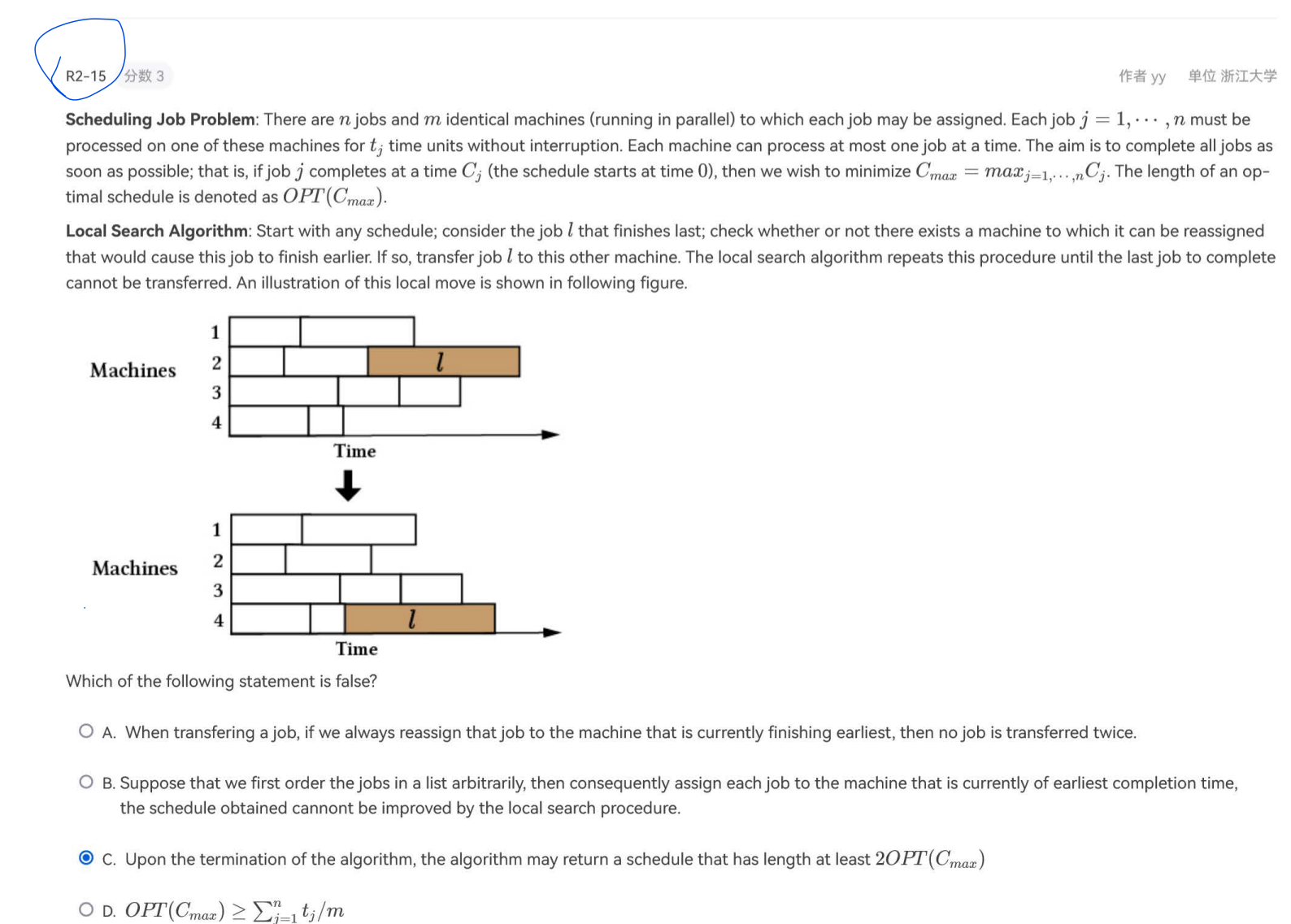
image-20240623142959766

[算法导论35-5]

随机算法

hiring problem

关键: 随机性 第\(i\)个人是最大的概率是\(1/i\)

Hire only once. 从前k个里选一个最大的，然后k+1~N依次跟最大值比，找到第一个>最大值的就break

给定k，求选到全局最大值的概率:

  • 假设i是最大值
    • hire i的概率是\(\frac{k}{i-1}\) (前i-1个人中的最大值落在前k个，否则就被hire走了)
    • i是最大值的概率是\(\frac{1}{N}\)

image-20240623134314406

每个人比前k个人好的概率都是一样的，就是\(1/(k+1)\)

quick sort

image-20240623111932028

(F)A randomized Quicksort algorithm has an O(NlogN) expected running time, only if all the input permutations are equally likely.

随机化快排的复杂度与输入无关

并行算法

image-20240624095424671

  • EREW:不实用
  • CREW:是经典的情况，读取用共享锁，写入用独享锁
  • CRCW:就是为了更加高效。我们对写入的数据进行判断，保证写入的数据是真实的

n数之和

\(T(n)=O(\log n),W(n)=O(n)\)

前缀和

前缀和 \(T(n)=O(\log n),W(n)=O(n)\)

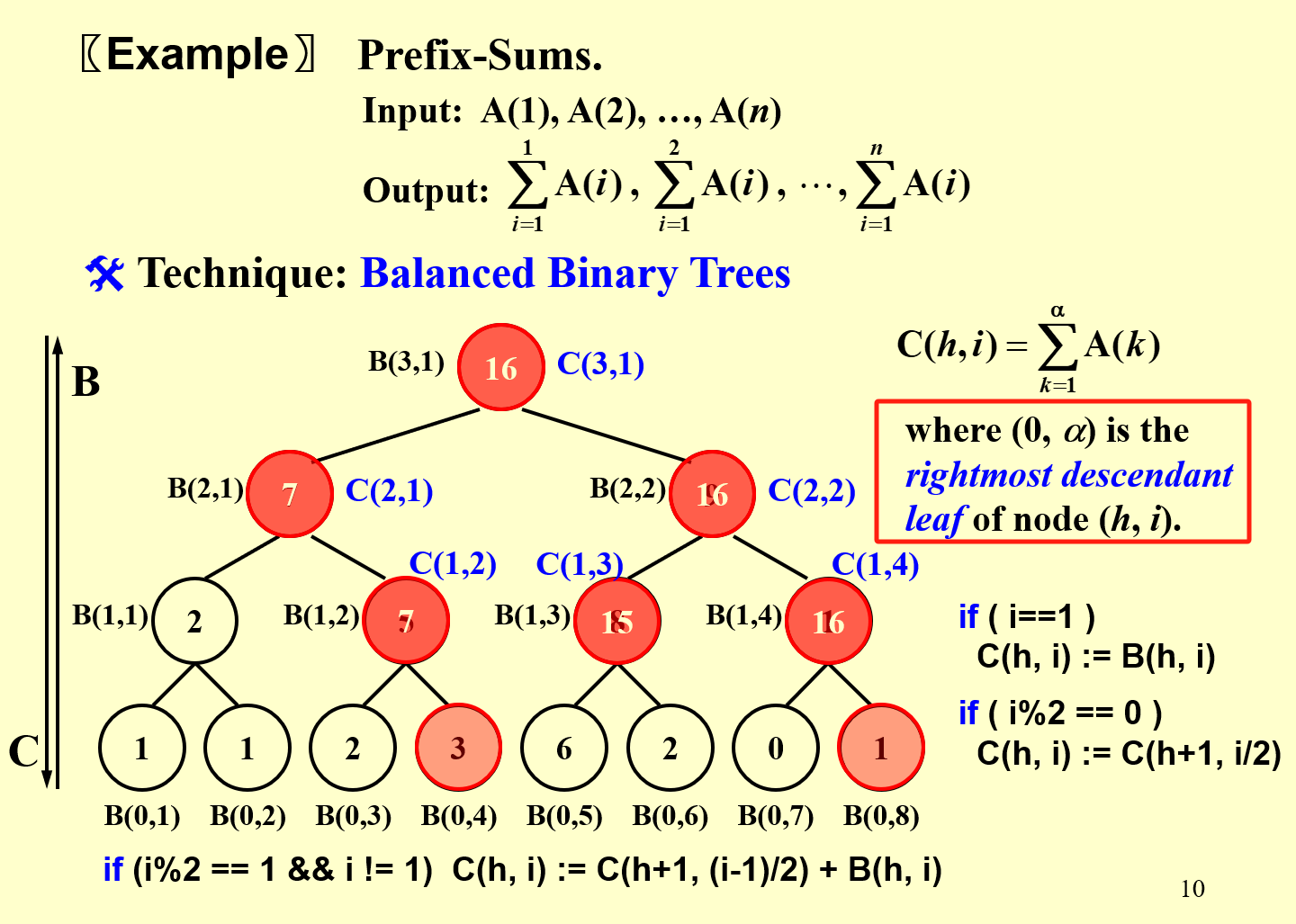
image-20240623095324227

归并(Ranking problem)

串行: \(T(n)=W(n)=O(n+m)\)

Parallel Binary search: 对每个数并行做二分查找,\(T(n)=O(\log n),W(n)=O(n\log n)\)

Parallel ranking 分成p=n/logn个段，每个段大小logn,同时做\(T(n)=O(\log n),W(n)=O(n)\)

image-20240623132947387

maximum finding

  • 用求和的方法
  • Compare all pairs \(T(n)=O(1),W(n)=O(n^2)\)
  • 分组 \(T(n)=O(\log \log n),W(n)=O(n)\)
  • random sampling \(T(n)=O(1),W(n)=O(n)\) with very high probability on CRCW

外排序

pass数量

要排序的有N个块，内存大小M个块, 使用k路归并

\(\boxed{\#\text{pass}= \lceil\log_k \lceil \frac{N}{M}\rceil\rceil+1}\)

Replacement selection: 需要一个长度为M的优先队列。开始时先把前M个数读入优先队列（排序)。之后对于每个输入的元素x:

  1. 把队头元素t出队。如果t没有标记,则t放到当前run. 如果t有标记,则新开一个run, 把新的run作为当前run
  2. 比较x和t
    1. 如果当前x<队头元素t, 说明x是下一个run的, 把x打一个标记，放到优先队列末尾。
    2. 否则说明x是当前run的,把x插入优先队列前面。

利用替换选择策略以后，每一次生成的 run 一定不小于M（末端余数除外），于是相对来说#pass就会减少

tape数量

朴素做法: k路归并需要2k个taoe

k路归并利用k阶斐波那契数列来切分: 需要k+1个tape 最大和最小的run是k阶斐波那契的相邻项

3 阶斐波那契: (0) 1 1 2 4 7 13 24

哈夫曼树优化：假设我们现在有若干个 run，并且我们将要进行 两两归并，那么我们可以根据每一个 run 的大小，根据霍夫曼树的规律来进行归并，即总是选最小的两个进行归并。

并行化: k路归并, 2k个input buffer, 2个output buffer

18-19期中

链接

1-2 其实势能分析只需要初始<=结尾，但是他说good, 那开始时就是最小值(?)

1-3 In a red-black tree, the number of rotations in the DELETE operation is O(1).

T. 红黑树插入最多2次旋转，删除最多3次

1-4 答案正确 得分: 4 / 4 Finding the maximum key from a splay tree will result in a tree with its root having no left subtree

T. 应该是no right subtree

1-5 可以

1-6 二项队列插入均摊\(O(1)\)

A queue can be implemented by using two stacks SA and SB as follows:

  • To enqueue x, we push x onto SA.
  • To dequeue from the queue, we pop and return the top item from SB. However, if SB is empty, we first fill it (and empty SA) by popping the top item from SA, pushing this item onto SB, and repeat until SA is empty.

Assuming that push and pop operations take O(1) worst-case time, please select a potential function ϕ which can help us prove that enqueue and dequeue operations take O(1) amortized time (when starting from an empty queue). (5 分)

让代价大的一步(empty SA) 势能降低。所以势能应该跟大小|SA|有关. 假设|SA|=k, 出队的时候代价\(c_i=k+k=2k\)(push,pop都要算) 要抵消这个代价\(\Phi_i-\Phi_{i-1}=-2k\) 所以势能函数\(\Phi=2|SA|\)

2-4 C

注意9 17 21的时候，先转17,再转9

2-8

C错误

A是对的 null path length 指的是节点x到空节点(类比红黑树的NIL,可能是叶子\也可能是只有一个孩子的节点)的距离

17-18期中

1-2 With the same operations, the resulting leftist heap is always more balanced than the skew heap.

T，左偏树是“左偏"的,本来就不平衡

1-6 In a red-black tree, an internal red node cannot be a node of degree 1.

T 黑高不相等了

Comments