Skip to content

1.Propositional Logic

Discrete Mathematics and Its Applications, Kenneth H. Rosen

有点鬼畜的Latex代码: \(\neg\)是\neg, \(\vee\)是\vee,\(\wedge\)是\wedge

1.1Propositional Logic

Propositions is a statement that is either true or false,but not both

Logic Operators

  1. Negation: \(\neg p\)
  2. Conjunction(and) \(p \wedge q\)
  3. Disjunction(or) \(p \vee q\)
  4. Exclusive or(xor)
  5. Implication(If p then q / p implies q / p only if q) \(p \to q\)

注意p only if q 也是 \(p \to q\)，相当于必要条件

p q p ->q
1 1 1
1 0 0
0 1 1
0 0 1

Everything implies true. False implies everything

  1. Biconditional : \(p \leftrightarrow q\)

1.2 Applications of Logic

Translating English Sentences

感觉在考英语

\(p \to q:\)

if p, then q.

p only if q

q unless \(\neg p\)

p is sufficient for q / q is necessary for p

q whenever p / q follows from p

To p,you must q

\(p \leftrightarrow q:\)

p is necessary and sufficient for q / ....and conversely/ p iff q

\(p \to q\)

  • converse: \(q \to p\)
  • inverse \(\neg p \to \neg q\)
  • contrapositive \(\neg q \to \neg p\)

Converse and Inverse are logically equivalant. Constrapositive and original proposition are logically equivalant

System Specifications

先翻译，然后转化成了给出一系列逻辑表达式，判断是否存在赋值的方法使得这些表达式全为True。先从单目入手，然后再考虑\(p\to q=F\)的时候可以确定赋值。如果\(p \to q=T\)，就枚举

Logic Puzzles

可以转化成逻辑表达式的方式，也可以直接枚举真值

1.3 Propositional Equivalences

Tautology: Compound propositions that are always true( e.g. \(p \vee\neg p\))

Contradiction: Compound propositions that are always false

Compound propositions that have the same truth values in all cases are called logically equivalent. \(p \equiv q\)

Logical Equivalences

Using truth tables, we can prove these equivalences:

\(p \vee 0=p \wedge 1=p\)

\(p \vee 1=1,p \wedge 0=0\)

De Morgan's Laws: \(\neg(p \wedge q)=\neg p \vee \neg q,\neg(p \vee q)=\neg p \wedge \neg q\)

Distribution: \(p \wedge(q \vee r)=(p \wedge q) \vee(p \wedge r)\)

​ \(p \vee(q\wedge r)=(p \vee q)\wedge (p \vee r)\)

注意有时也反向用分配律合并同类项

Absorption Laws: \(\boxed{p \vee(p \wedge q)=p, p \wedge(p \vee q)=p}\)

implication law:

\(p \to q \equiv \neg p \vee q\)

(Because p implies q is false only if p=1 and q=0)

Then using these laws we can prove:

Conditional statements:

\(p \to q \equiv \neg q \to \neg p\)

\(\neg(p \to q)=p\wedge \neg q\)

Biconditional statements:

\(p \leftrightarrow q \equiv (p \to q)\wedge(q\to p)\)

\(p \leftrightarrow q \equiv \neg p \leftrightarrow \neg q\)

\(p \leftrightarrow q \equiv (p \wedge q)\vee(\neg p \wedge \neg q)\)

第三条从真值表来看是显然的。但是也可以用上面的定律证,多次用分配律拆括号,然后用\(p \wedge \neg p=0\)的性质

16e787cd097c97b41794fd24cbcfbecf.png

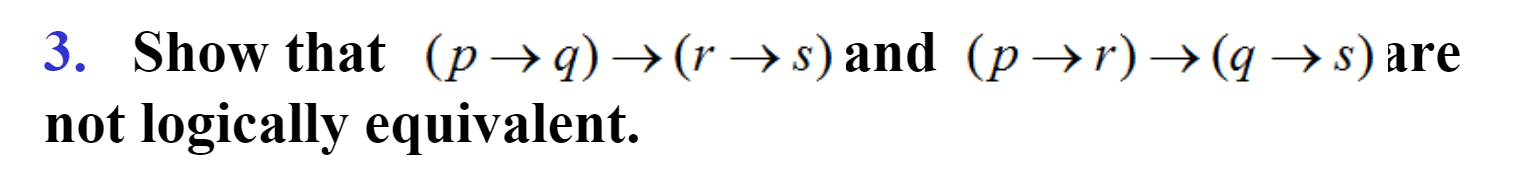
90b008e6b1bf4c41db72f664d6beaad4.png

Assume that the second proposition is false. Then \(q \to s=F,p \to r=T\). so \(q=T,s=F\). Enumerate all 3 cases of \(p,r\), then we can get \(p=F,q=T,r=F,s=F\) as a counterexample.

Satisfiability

A compound proposition is satisfiable if there is an assignment of truth values to its variables that makes it true

Normal Form

Literal: \(p\) or \(\neg p\)

Distributive Normal Form (DNF) : A formula is said to be in disjunctive normal form if it is written as a disjunction, in which all the terms are conjunctions of literals(a variable or its negation). etc. \((p \wedge \neg q)\vee r\). We can also define Conjunctive Normal Form(CNF) 2e8077e251d71b7d0162226fca6b7375.png

d7d678adc8f3d20a71bfee418da7942a.png

A minterm is a conjunction of literals in which each variable is represented exactly once. For\(p,q,r\) \(p \wedge q\) s not a minterm. \(p \wedge q \wedge r\) is a minterm.

\(2^n\) minterms.

Transforming into Full DNF:First \(\wedge(p \vee \neg p)\), then use distributive law

2b401fa3fed571b89920f5aec6a0989a.png

Full DNF can be used to construct a proposition with a given truth table. etc. proposition consisting of 3 variables p,q,r is true when exactly two variables are true. \((p \wedge q\wedge \neg r)\vee(p \wedge \neg q\wedge r)\vee(\neg p \wedge q\wedge r)\). Therefore, every compound proposition is logically equivalent to a full DNF.

  • Each minterm is true for exactly one assignment

  • minterm \(A,B,A\neq B \to A\wedge B=F\)

  • Same Full DNF \(\leftrightarrow\) Logically equivalent.

A collection of logical operators is called functionally complete if every compound proposition is logically equivalent to a compound proposition consisting of only these operators.

For example

  • \(\neg\) and \(\wedge\) form a functionally complete collection.

  • \(\downarrow\)(NOR \(\neg(p \vee q)\)) is a functionally complete collection. \(|\)(NAND) is functionally complete.

  • \(p \downarrow p \equiv \neg p, (p \downarrow q)\downarrow(p\downarrow q)=\neg(p\downarrow q)=p\vee q\)

1.4 Predicates and Quantifiers

Predicates

A predicate (propositional function) is a statement that contains variables. Once the values of the variables are specified, the function has a truth value.

\(P(x_1,x_2\dots x_n)\) is called n-ary or n-place predicate. such as \(P(x)= x>0\)

Quantifiers

Universal Quantifier: \(\forall x\ p(x)\) Existential Quantifier: \(\exists x\ p(x)\)

Domain (domain of discourse / universe of discourse): range of the possible values of the variable x

Precedence: \(\forall\) and \(\exists\) have higher precedence than all logical operators

Precedence Operators
1 \(\forall,\exists\)
2 \(\neg\)
3 \(\wedge,\vee\)
4 \(\to,\leftrightarrow\)

\(\forall x P(x) \vee Q(x) \equiv (\forall x P(x)) \vee Q(x)\)

Binding Variables

Bound variable: a variable is bound if it is quantified.

All the variables in a propositional function must be quantified or set equal to a particular value to turn it into a proposition.

Logical Equivalences Involving Quantifiers

Distribution:

\(\forall (p(x) \wedge q(x)) \equiv\forall x p(x) \wedge \forall x q(x)\)

\(\exists (p(x) \vee q(x)) \equiv \exists x p(x) \vee\exists x q(x)\)

note that **you cannot distribute Universal Quantifier over OR **

De Morgan's Law: \(\neg (\forall x\ p(x)) \equiv \exists x \ \neg p(x)\) \(\neg (\exists x\ p(x)) \equiv\forall x \ \neg p(x)\) 注意右推左在证明里很常用 (1) \(\quad \forall x P(x) \vee A \equiv\forall x(P(x) \vee A)\) (2) \(\forall x P(x) \wedge A \equiv \forall x(P(x) \wedge A)\) (3) \(\quad \exists x P(x) \vee A \equiv \exists x(P(x) \vee A)\) (4) \(\exists x P(x) \wedge A \equiv \exists x(P(x) \wedge A)\) (5) \(\quad \forall x(A \rightarrow P(x)) \equiv A \rightarrow \forall x P(x)\) (6) \(\exists x(A \rightarrow P(x)) \equiv A \rightarrow \exists x P(x)\) (7) \(\forall x(P(x) \rightarrow A) \equiv \exists x P(x) \rightarrow A\) (8) \(\quad \exists x(P(x) \rightarrow A) \equiv \forall x P(x) \rightarrow A\) where the truth value of \(A\) is not related to

记忆方法：除了A做结果的时候改变量词，其他与、或等都可以直接提出括号

Proof: (1)-(4) Discuss the truth value of A (5)-(8) Use the implication law

\(\exists x (\neg P(x)\vee A)=\exists x \neg P(x) \vee A=\neg(\forall x P(x))\vee A=\forall xP(x) \to A\)

\(\exists x (P(x) \to Q(x))=\exists (\neg P(x) \wedge Q(x))\)

1.5 Nested Quantifiers

\(\forall x \exists y P(x,y) \neq \exists x \forall y P(x,y)\). etc. \(P(x,y)=x\) loves \(y\)

Negation: 交换符号、最后的条件否定

Prenex Normal Form:

b57e71faf9ccc5ca734fd0c945a10e74.png

  1. Get rid of arrowsImplication Law
  2. Move negative
  3. Change names
  4. To the front

Translating from English to Quantifiers

etc. All lions are fierce

\(\forall x(P(x) \to Q(x))\), where the domain of \(x\) is all animal

Note that we can't write \(\forall (P(x) \wedge Q(x))\), which means all animals are lions and all animals are fierce

Some students in the class have visited Mexico

\(\exists x(P(x)\wedge Q(x))\), where the domain of \(x\) is all people

Note that we can't write \(\exists (P(x) \to Q(x))\), because there can be \(x\) that \(P(x)=F,Q(x)=T\)

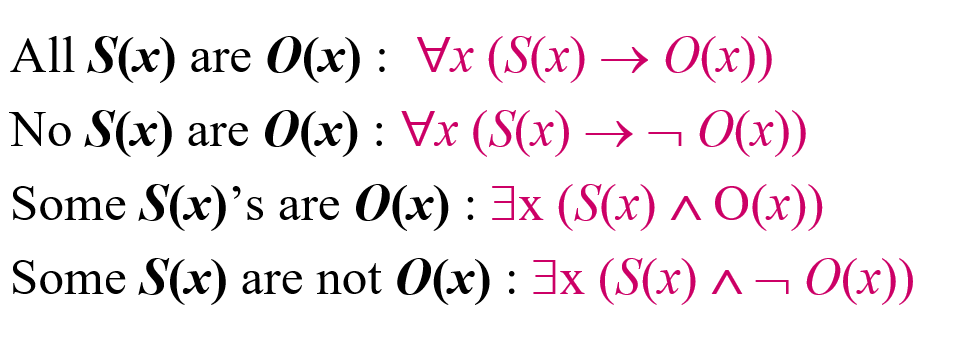
c53c25b3a4abd562faf25c82fc8a7f2e.png

Nested Quantifiers

There is only one \(x\) that \(P(x)\). \(\exists x\forall y(x=y\leftrightarrow P(y))\)

or \(\exists x\forall y(P(x)\wedge(x\neq y \to \neg P(y)))\)

Everyone except one \(x\) that \(P(x)\). \(\exists x\forall y(x\neq y\leftrightarrow P(x))\)

There is at least 2 \(\exists x \exists y (x \neq y \wedge P(x) \wedge P(y))\)

8843f1a6e3bc564354568972396f41d3.png

180dd8a23a5e5c5f9499f808d5aa5d13.png

翻译成英文之后不要出现x,y,z等字母

1.6 Rule of Inference ☆

Argument: A sequence of propositions: If \((p_1 \wedge p_2 \dots \wedge p_n)\to q\) is tautology, then the argument is valid

Formal Form(考试时注意格式!不要忘了写∴)

\[\begin{aligned}&p_1\\&p_2\\\ &\dots\\&p_n\\ &\_\_\_\_\\ ∴&q \end{aligned} \]

Trick: \(p_1\dots p_n(\text{premises}),(q \to r)(\text{conclusion}) \equiv p_1\dots p_n,q(\text{premises}) ,r\)

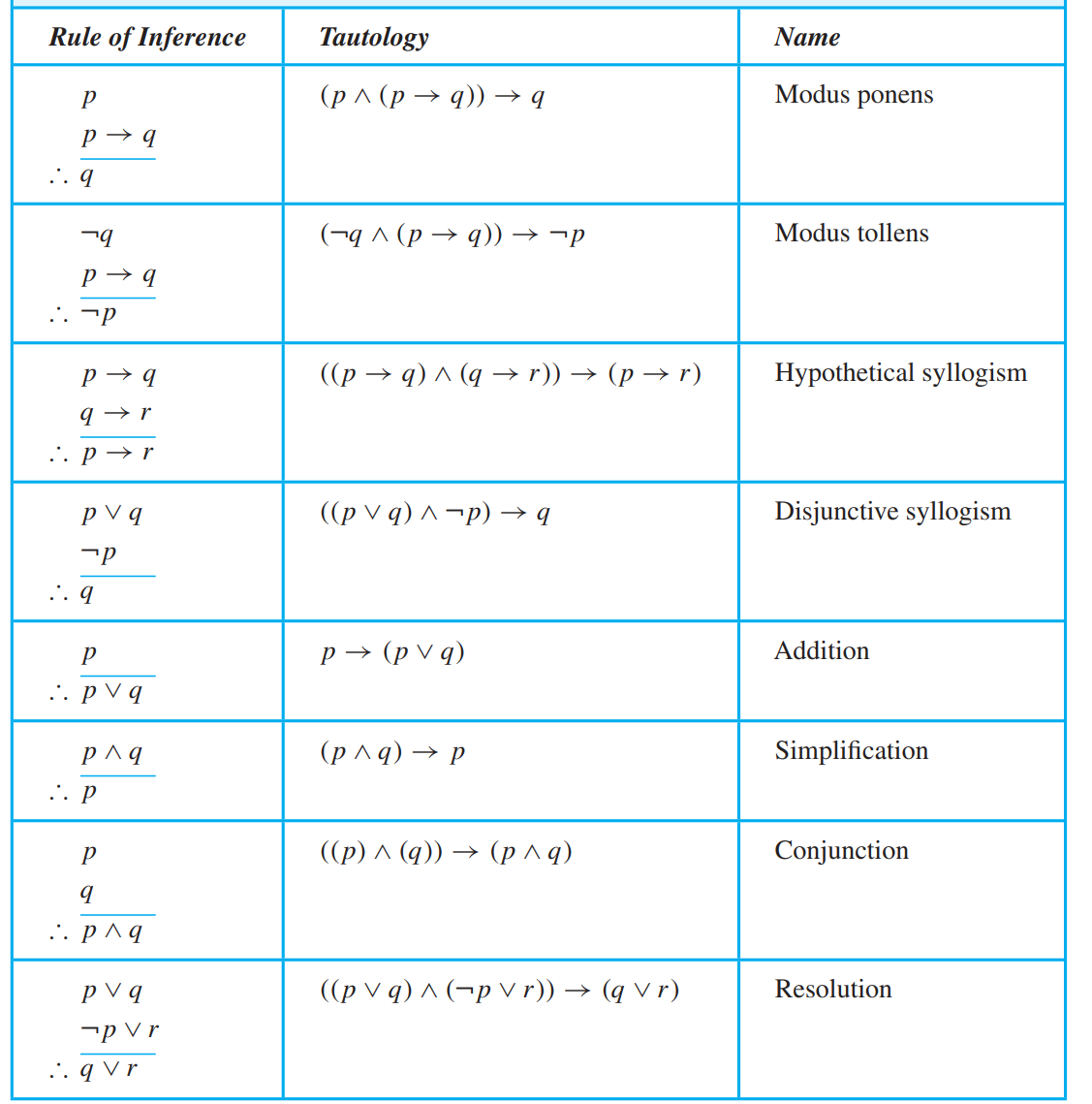
bcef9efa3a970384b1881020a6a864f2.png

83fff811ac4e39ab9753856590b348a5.png

Resolution:

\[((p \vee q)\wedge(\neg p \vee s)) \to (q\vee s) \]

\(p \vee q,\neg p \vee r ,\neg q \vee s\). 先对1,3，再对2用resolution

Rules of inference for Quantified Statements

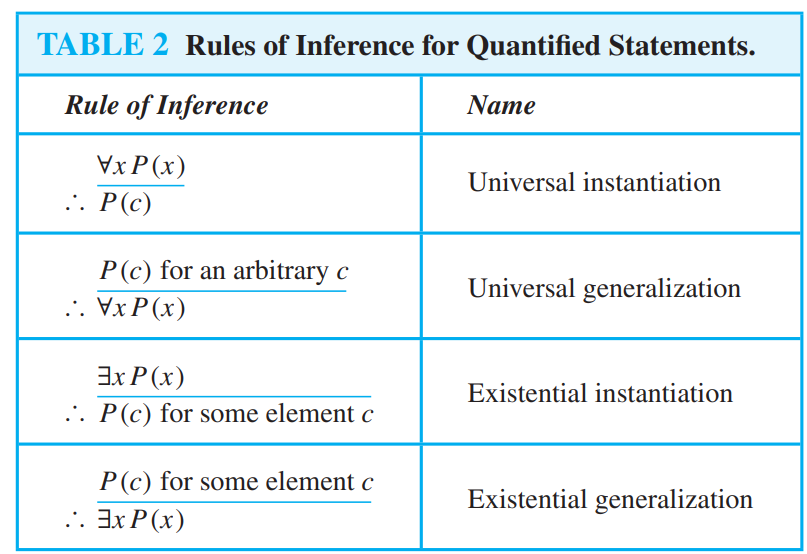
970e28c212d724abce7c882c87ebba1f.png

A:\(\forall x \exists y P(x,y)\) B:\(\exists x\forall y P(x,y)\) A不能推出B，B可以推出A

Proofs

Terminology: - theorem 定理 - axioms 公理 - lemma 引理 - corollary 推论 - conjecture 猜想

Vacuous proof: \(p=F,p \to q=T\). Trivial Proof:\(q=T\)

Proof by contraposition:

\(p \to q \equiv \neg q \to \neg p\)

Assume that \(\neg q\) is true

Proof by contradiction:

Assume that \(p,\neg q\) is true, deduce \((p \and \neg q)\to \neg p\), \(p \and \neg p\) forms a contradiction

Proof of equivalence.

Comments