Skip to content

ICS Chapter 1 3

Chapter 1

(1.3.1)The notion of Abstraction

hardware/software

(1.5)Two important ideas:

  • All computers are capable of computing exactly the same things if they are given enough time and enough memory.

  • It is necessary to transform our problem from the language of humans to the voltages that influence the flow of electrons.(language of computer)

    • Problem:ambiguity of natual languages
    • Algorithm: a step by step procedure, each procedure have 3 properties: (离散数学中讲过)
      • effective computability:each step can be carried out by a computer
      • definiteness:each step is precisely defined
      • finiteness:the procedure terminates after a finite period of time.
    • Programming Language
      • high level: Python,C++...
      • low level: Assembly
      • Compiler: High-level Lang. -> Intermediate Form -> ISA
    • ISA: Instruction Set Mechanism
      1. opcodes: operations the computer can perform
      2. data types: acceptable representations for operands
      3. addressing modes: mechanisms that the computer can use to figure out where the operands are located
    • Microarchitecture: is the digital logic that allows an instruction set to be executed. (implementation) ISA是抽象的指令（类似于接口），而microarchitecture是搭建电路实现这些指令
    • Logic Gates
    • Circuits

    从最顶层的Problem到最底层的circuits，就是从具体到抽象

Chapter 2(重点)

Integer representation

  • Signed Magnitude 原码
  • 1's Complement 反码
  • 2's Complement 补码

补码转原码: 取反+1

补码加法: 符号位也参与运算，符号位的进位不要管

范围\([-2^{\color{red}n-1},2^{n-1}-1]\)

不同长度补码的转换：正数前面补0，负数前面补1 (有符号拓展,SEXT)

(HW1 2.17):0101+110=0101+1110=0011=3

溢出(overflow): 用二进制判断: 符号位前的进位和符号位后的进位不同，则溢出

(HW1 2.20)

16进制补码:如果是正数,直接转16进制,前面加x. 如果是负数,那么就以转完16进制后的长度(4*k)做补码

(HW2 2.48)

Floating point

32-bit(float)

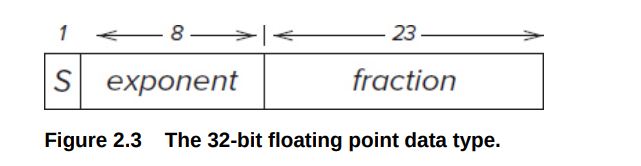
2106ee4b4d56dd18596d847f8d344aee.png

(16bit: 1 / 5 / 10 64bit: 1/11/52)

  • 8位的exponent是无符号的，范围是\([0,255]\)
  • 23位的fraction

当\(1 \leq \text{exponent} \leq 254\) (Normalized Form)

\(\boxed{N=(-1)^S\times 1.\text{fraction}\times 2^{\text{exponent}-127},1 \leq \text{exponent} \leq 254}\)

绝对值最小 \(1.0000...0\times 2^{-126}=2^{-126}\)

绝对值最大 \(1.1111\dots 1\times 2^{127}\approx 2^{128}\)

(2.40) 1 10000000 10010000000000000000000

\((-1)^1\times 1.1001\times 2^{128-127}=-3.125\)

当\(\text{exponent}=255\) (infinities)

​ 用来表示无穷. 如inf就是exponent=255,fraction全0. 如果exponent=255,fraction不是全0,就是NaN

当\(\text{exponent}=0\) (subnormal numbers)

​ \(N=(-1)^S\times 0.fraction \times 2^{-126}\)

​ 最大\(0.111\dots1\times 2^{-126}=(1-2^{-23})\times 2^{-126}\)

​ 最小\(0.000\dots 1\times 2^{-126}=2^{-149}\)

​ 注意这里是0.fraction,而不是Normalized Form中的1.,且指数换成了-126. 去掉要求的1,这样可以表示的指数范围就从-127变到了-149。

Digital Logic Structures

Transitors

PMOS \(U_G-U_S<-1.2V\)导通 一般作上管(和\(U_S=1.2V\)相连,此时若\(U_G=0\)则导通)

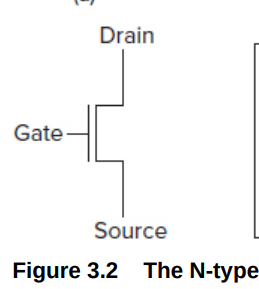
N-type \(U_G-U_S>1.2V\) 一般作下管(接地\(U_S=0\),此时若\(U_G=1.2V\)则导通, \(U_G=0\)则断路 2fd37cd1ddadaa60dbf3dafe6fb140b0.png

Gates

NOT Gates

横线代表正极，三角形代表接地

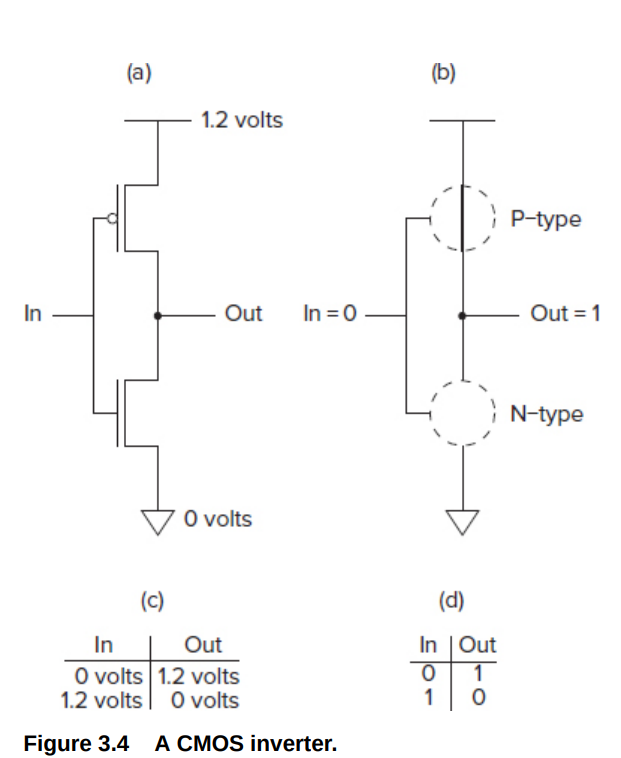
57f604bf7952bc0a752645e60832a52d.png

NOR/OR

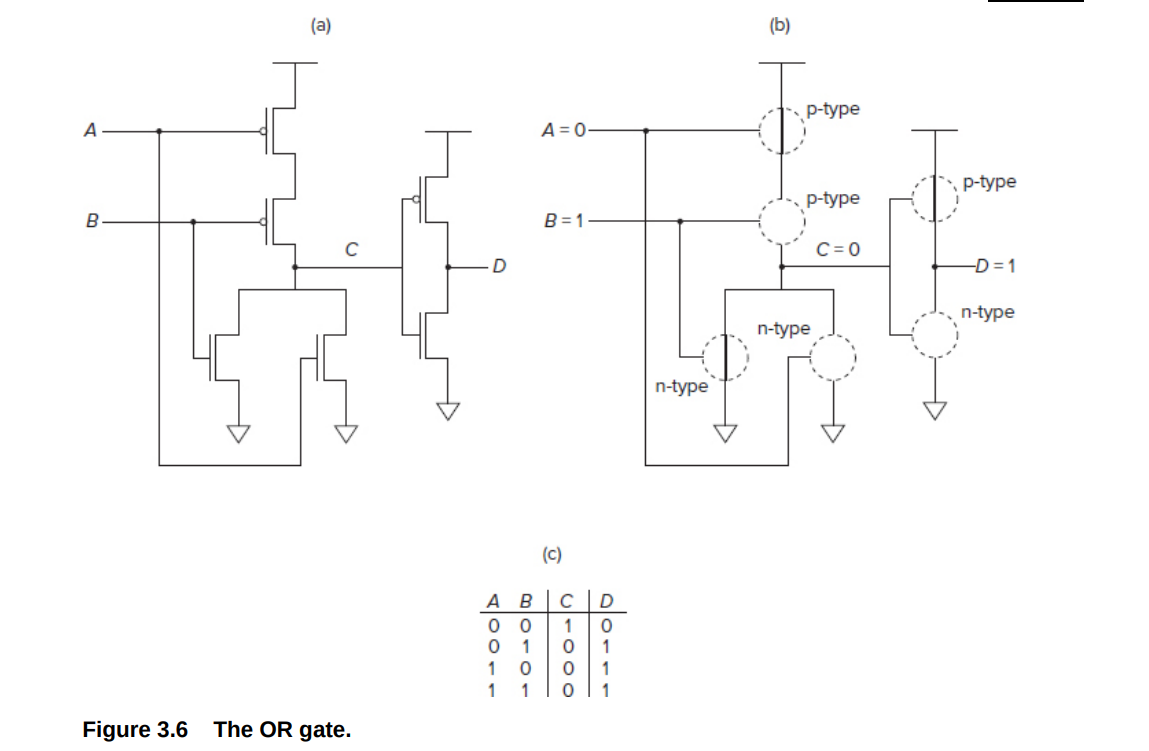
264b761579d5a04d18350a2e2c10127f.png

OR=NOR+NOT,所以只需要看左边的NOR

NOR，当且仅当输入是两个0的时候为1, 因此上面用两个P-type串联,仅两个都是0的时候导通，输出为1。下面用两个N-type并联，只要有1个为0的时候就导通接地，输出为0。

上半部分选择什么时候高电势(1)，下半部分选择什么时候接地(0) 串联代表"与" 并联代表"或"

如果是多个输入,只需要把多个输入串联起来或者并联起来即可。

NAND/AND

同理对于NAND,只要输入有1个0,输出就为1,所以上面用两个P-type并联, 下面用两个N-type串联

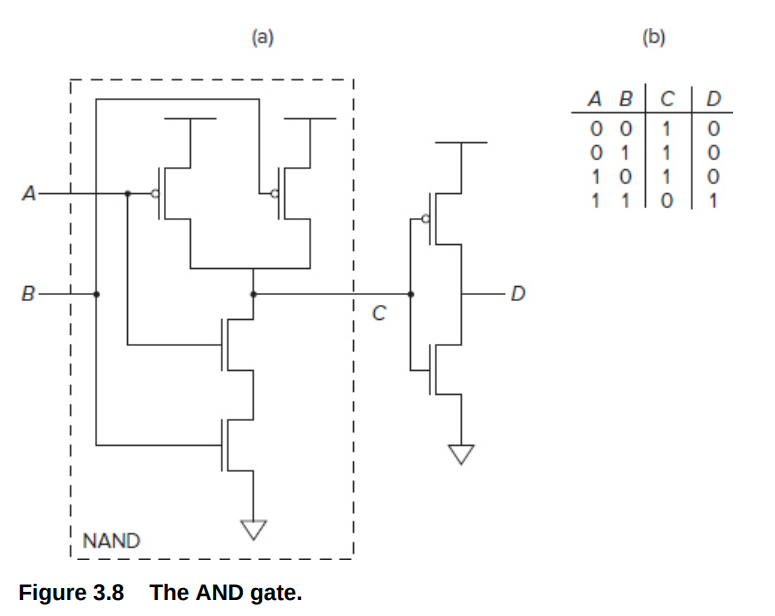
3f46cad5c5f3452ee012c6a5217721d6.png

Combinatorial Logic Circuits

对前面半导体的结构进行进行封装，就得到了常见的逻辑门，符号如下

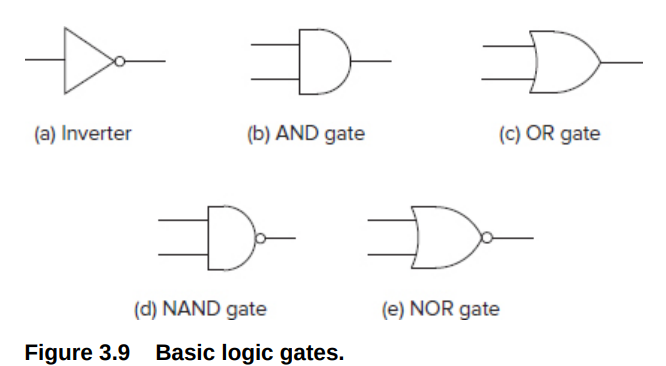
ba2b91822a9823e4689ec24c91aaa238.png

NOT Gate有时也简化成一个小圆圈.

表达式： \(A+B\) 表示\(A\) OR \(B\). \(AB\) 表示 \(A\) AND \(B\) \(\bar{A}\) 表示 NOT \(A\)

Decoders

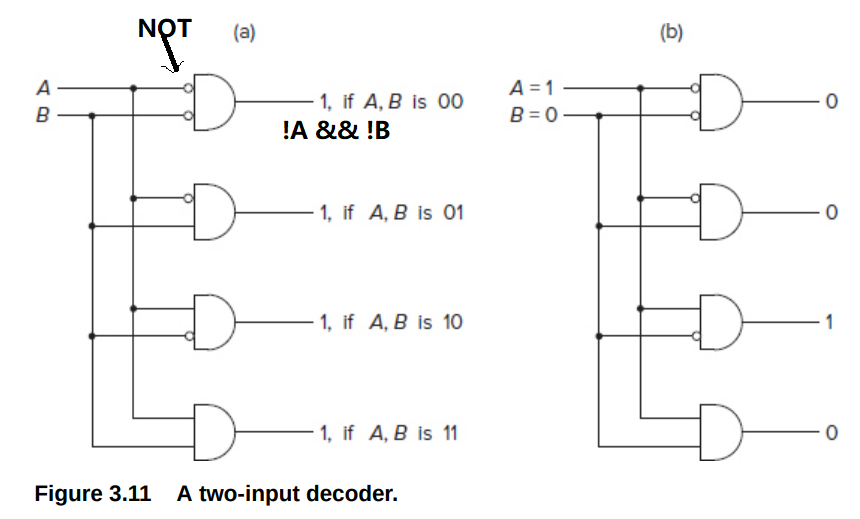
30bff5f77fcb810d4a323c181765b402.png

用AND和NOT组成(注意前面的空心圆圈代表NOT)

分类所有输入的组合。可用于解析opcode

MUX

  • \(2^n\) inputs, 1 output, n select lines

通过S来选择对应的输入

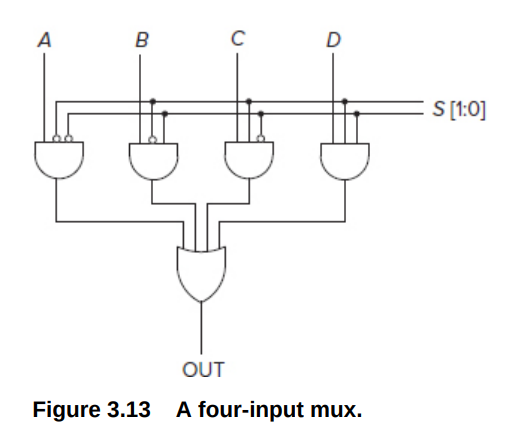
f5220d8c19b9e70391c67637ff2333e7.png

S=00,01 10 11 分别输出A,B,C,D

1-bit adder

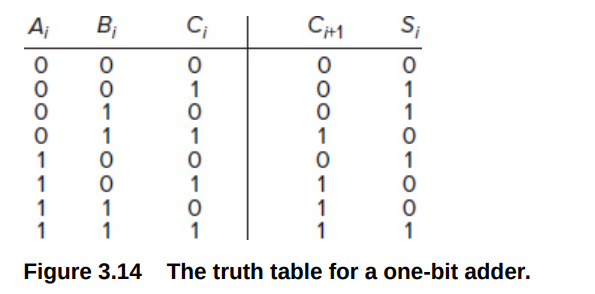
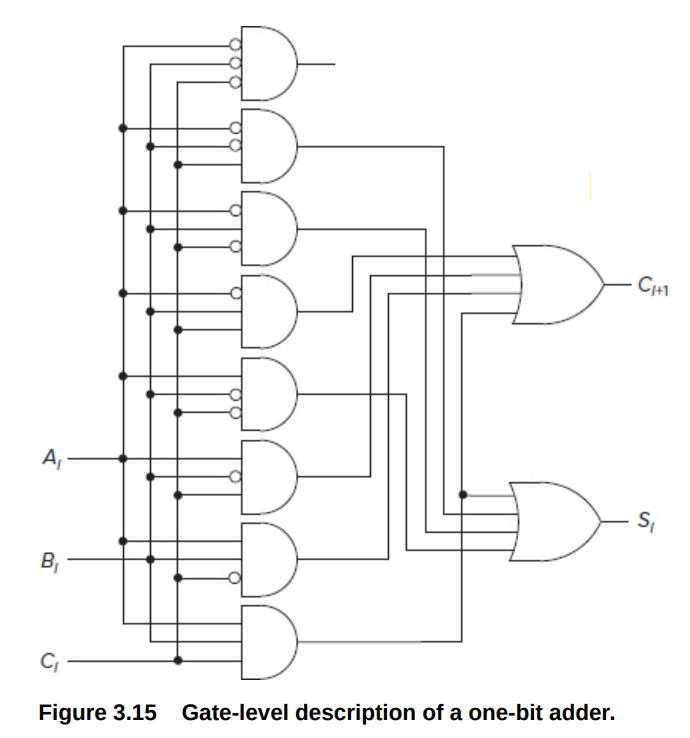
本质上也是decoder,对输入的\(A_i,B_i,C_{i-1}\)输出对应的\(S_{i},C_{i}\). 如果为1就连向对应的输出 29e77610dd07044f3c90708db8abfcd7.png 82c7aab9f054268cee1f1cdc611841a7.png

从上到下对应000,001...111

The Programmable Logic Array (PLA)

对1-adder进行进一步抽象, 相当于decoder+内部自定义连接+一系列or gates

这种思路很重要。对于一些过程，如比较，加法等，我们不需要关心实现思路，只需要列出真值表然后用PLA解析即可。对于n-bit输入,m-bit的输出, 对于每一个输入\(x\)(共\(2^n\)个), 对应输出\(y\), 把\(x\)对应的AND Gate 连向 \(y\)中为1的bit对应的OR Gate

Patt在这本书中强调的是更简单的去设计逻辑电路，而不是追求用更少的逻辑门

HW2 3.3

Storage Elements

R-S latch

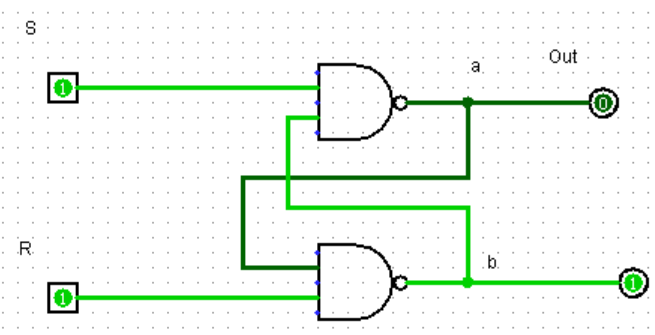
ff471d86f424e7d669dde75baae5a134.png

R = S = 1:hold current value in latch (Out can be 0 o)

S = 0, R=1:set value to 1 (set)

R = 0, S = 1:set value to 0 (reset)

R = S = 0(•Don’t do it!)

•both outputs equal one

•final state determined by electrical properties of gates

Gated D latch

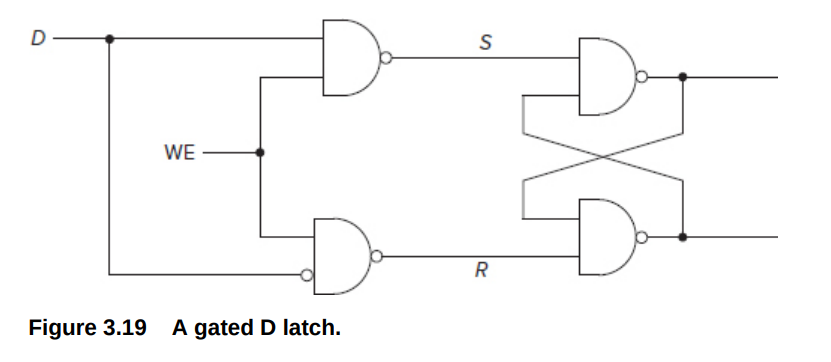
29452ca5fd2a2a4c6b873ddebfd7e3ba.png

WE=0, S=R=1 no matter what D equals to(Write is not enabled, store the previous state)

WE=1(Write Enable, Set the value to D)

D=1,S=0,R=1,Out=1 D=0,R=0,S=1,Out=0

Prevents S=R=0

Memory

address space:the total number of uniquely identifiable locations addressability: The number of bits stored in each memory location

\(n\) bits of address, \(2^n\) locations in the address space. \(A\)代表地址 \(D_l[2:0]\)代表要写的值 \(D[2:0]\)代表要读的值

每一行对应一个地址,每个gate D latch存储一位二进制

decoder用于选择对应的行

mux用于读出latch里面的值

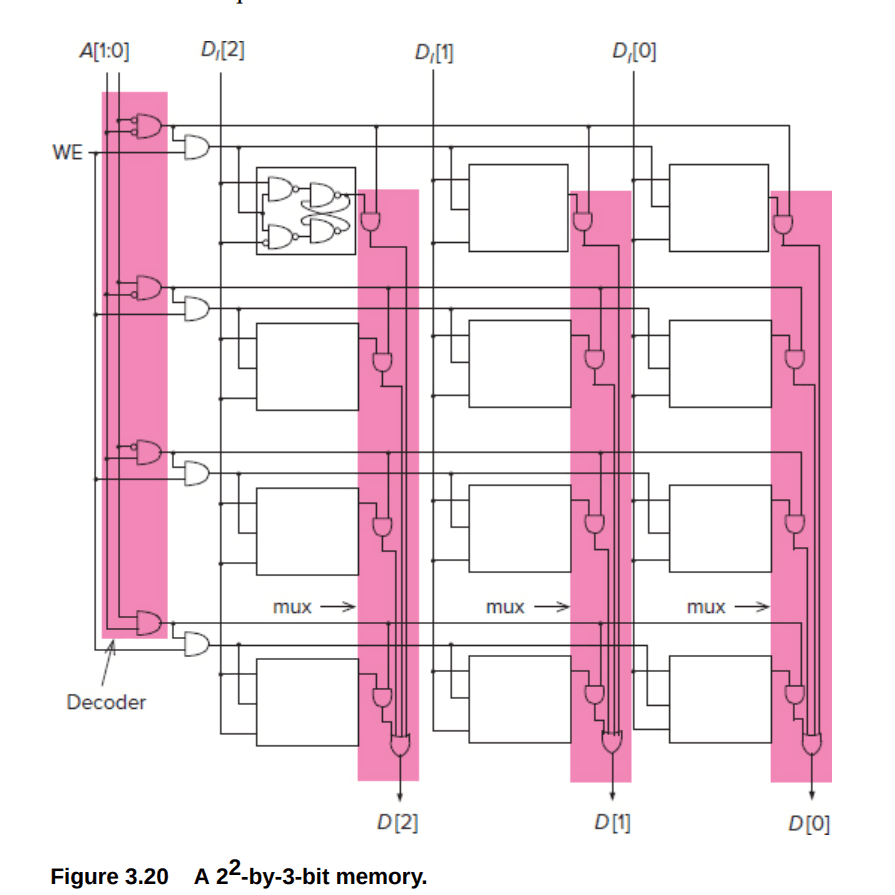
4bdc5c4d8b8c3ffd584d8763c0a619de.png

左边第一列是用来选写的行 其余是用来的

Finite State Machines

Synchonous Finite State Machines

the clock is a signal whose value alternates between 0 and 1.

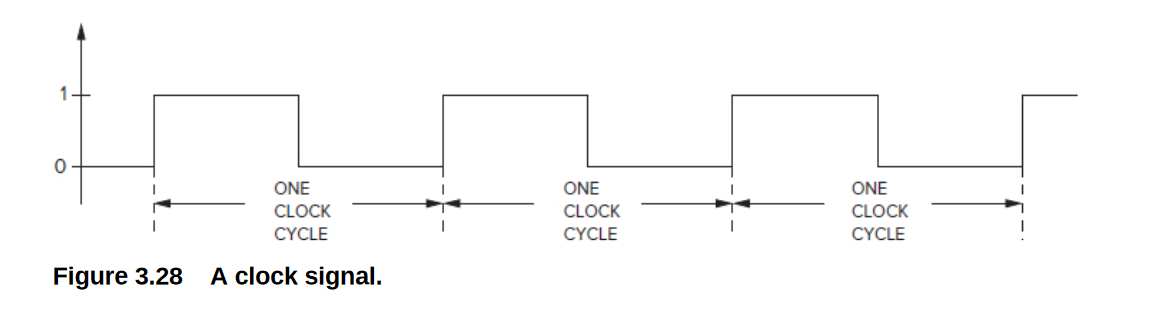
a49c10f59e56223fcc3bb75f69e5b1fd.png

synchronous:the state transitions take place, one after the other, at identical fixed units of time

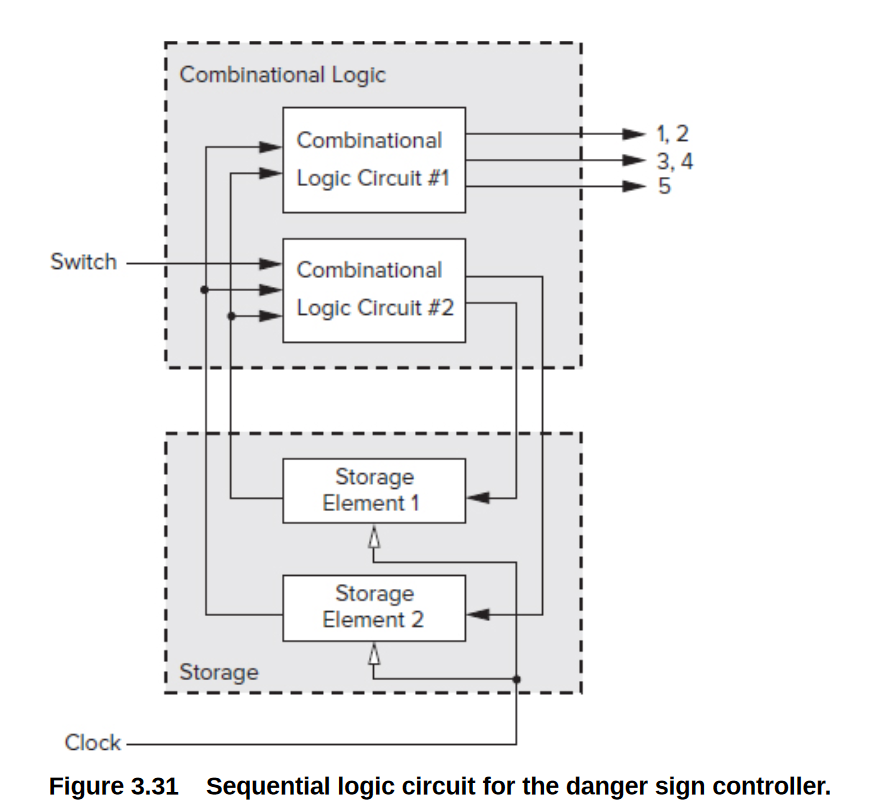
645ea00603f889835e89f3735a07b724.png

原理:Combinational Logic Circuit #1是输出模块

Combinational Logic Circuit #2 本质上是一个PLA, 输入是状态机的当前状态和开关Switch，输出的是状态机的下一个状态，状态编码存储在Storage里

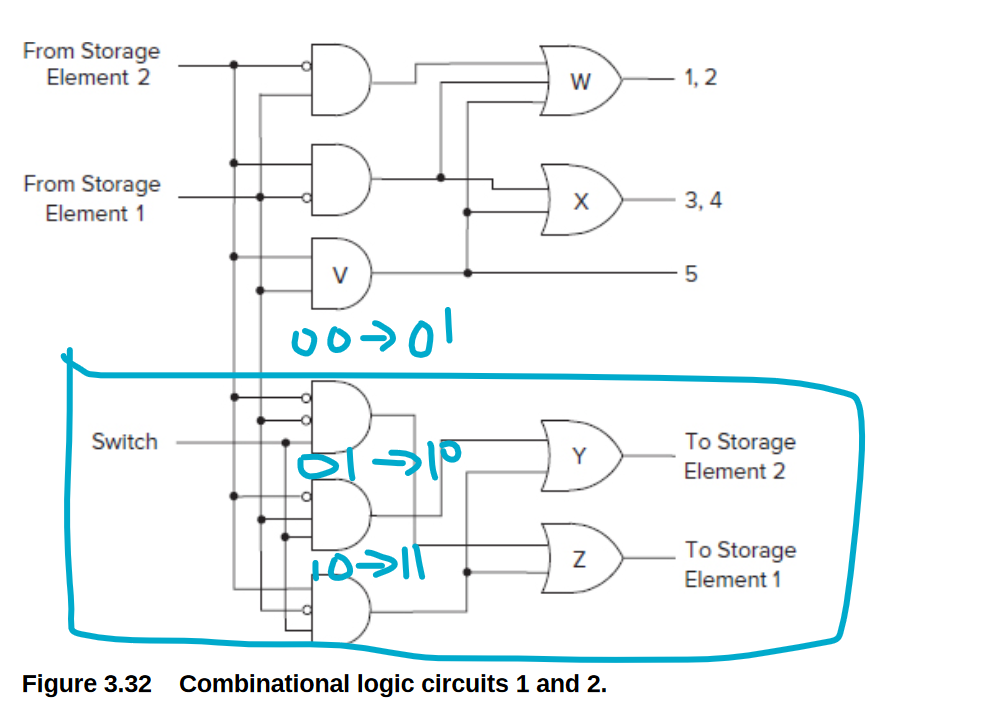
ee3b57253fe5216fd560b925d4a3b9c3.png

把状态机的变化关系(带时序的真值表) 画成电路

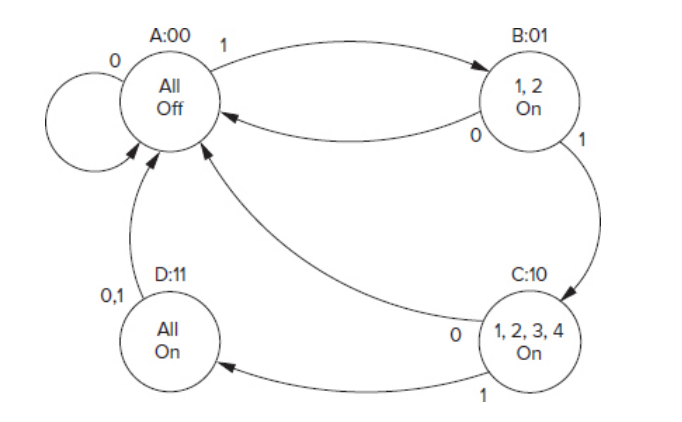
03eed3f4a2a0930aa2bf2dac93b250ca.png

状态机: - 点上要写状态\(S\) - 线上写输入\(X\)表示状态转移 - 输出如果和输入无关，就写在点上。否则写在输入后面

Flip-Flop

防止状态快速变化

We do not want the input to the storage elements to take effect until the end of the current clock cycle.

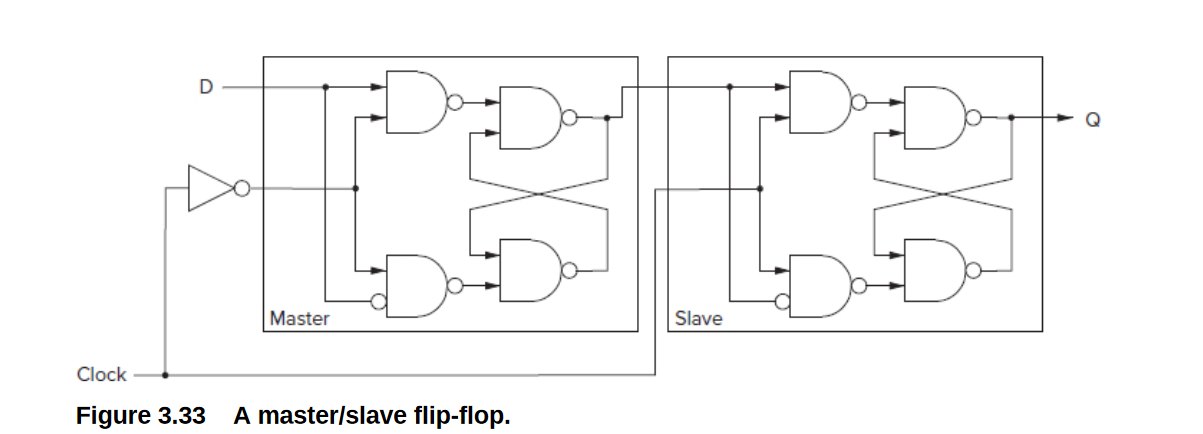
06bed1c0a9cfa9e906c8eec204c8f67a.png

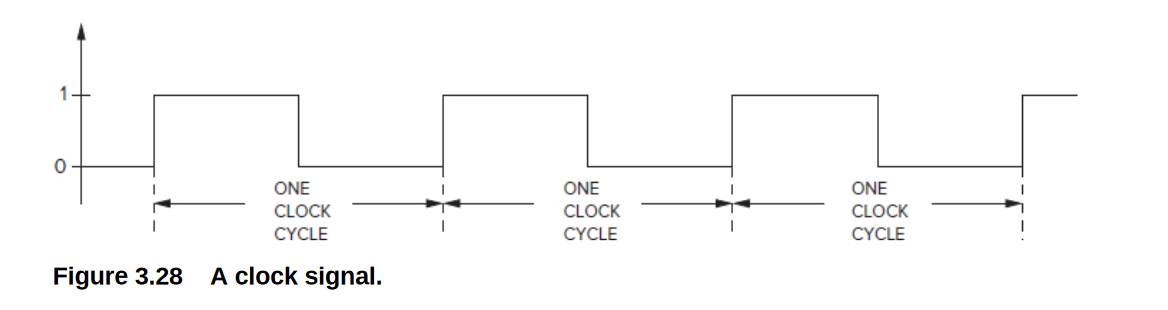
10857f49b65f26915bedf492bfc44d28.png

原理:

  • 在时钟周期的前一半(A),Clock=1, Master不可写,Slave可写, Master存储的状态\(S_n\)被写入Slave
  • Combinatorial Logic根据Slave的状态\(S_n\)计算\(S_{n+1}\)
  • 在时钟周期的后一半(B),Clock=0,Master可写,Slave不可写,新的状态\(S_{n+1}\)被写进Master, 下一个时钟周期再进入Slave

​ Master起到了缓存下一个状态的作用

Comments