Skip to content

公钥密码学

概念: 公钥\(PU\),私钥\(PR\)

加密/解密: 发送方用接受方的公钥进行加密

cd6f48ca056f58632193af1d73b30d80.png

数字签名: 发送方A用私钥加密，接收方B用A的公钥解密 (没有保密性,因为所有有A的公钥的人都可以解密)

Diffie-Hellman

原根

原根

p是质数 \(\bmod p\)下的原根: \(g\bmod p,g^2\bmod p,\dots g^{p-1} \bmod p\)是\(1\dots p\)的全排列

\(A=g^a \bmod p\) 已知\(A,g\),求\(a\)的复杂度

方法

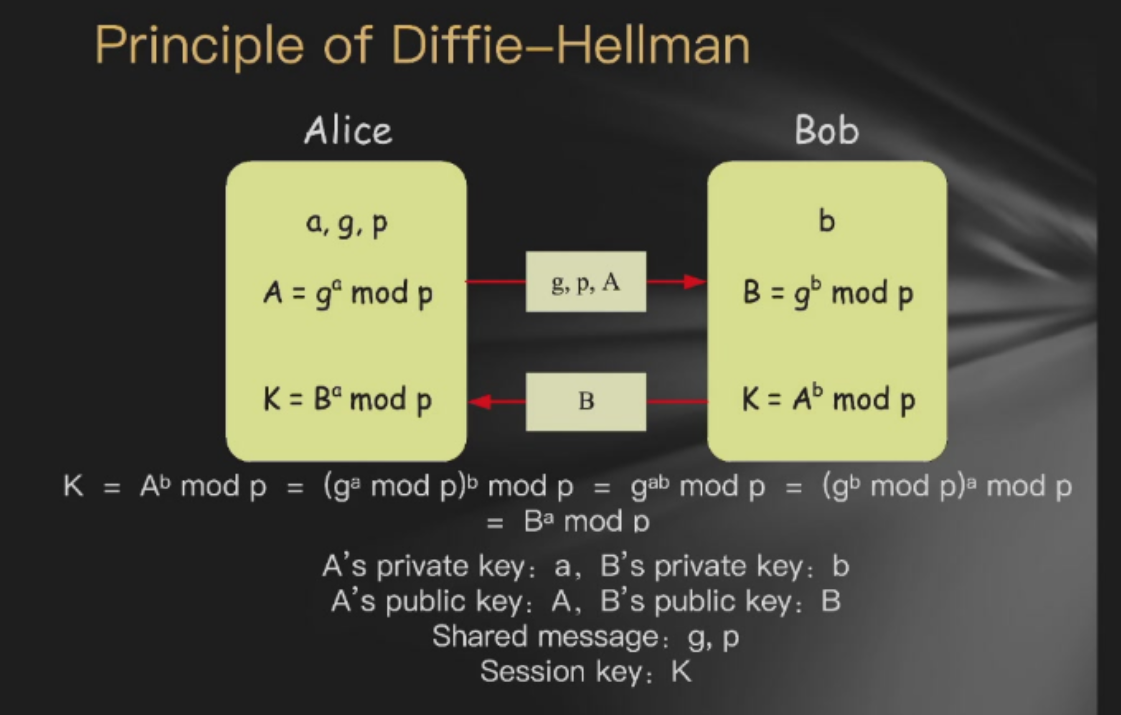
36d8c3ccc2e6c2ed759a54e03b30dfac.png

分析

  1. 不是加密算法，一般用来交换密钥K(因为攻击者只知道g,p,A,B), 不知道a,b

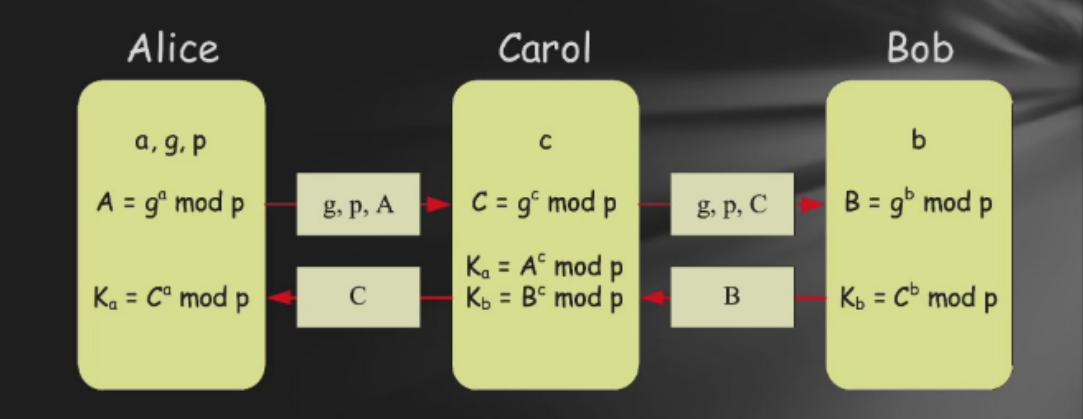
  2. 缺陷: 中间人攻击 用自己的c替换a 已知g,p

    5ee071a8ea20777354c6591a77a7e872.png

RSA

单向函数: n不能分解成p

Key generation

  1. 选择两个大质数\(p,q\) \(n=pq\) (用miller-rabin)
  2. 找两个数e,d: 满足\(ed \bmod (p-1)(q-1)=1\) (用扩展欧几里得)
  3. \(PB=(e,n),PR=d\)

加密解密

  • 加密 \(c=m^e \bmod n\)
  • 解密\(m=c^d\bmod n\)

证明: \(\varphi(n)=\varphi(p)\varphi(q)=(p-1)(q-1)\)

  • 如果m,n互质 \(m^{ed}\mod n=m^{h\varphi(n)+1}\mod n=m\bmod n\) (欧拉定理)
  • 如果m,n不互质, m是p或q的倍数
    • 如果m是p的倍数 \(m^{ed}=0=m(\bmod p)\)
    • 如果m不是p的倍数,m,p互质，\(m^{p-1}=1(\bmod p),m^{ed}=m^{k(q-1)(p-1)+1}=m(\bmod p)\)
    • 所以\(m^{ed}=m(\bmod p)\), 同理\(m^{ed}=m(\bmod q)\)

数字签名

  1. 验证签名者、日期、时间
  2. 验证消息内容
  3. 第三方仲裁

095d51e648d6c9b3429638e5730e0bc7.png

明文-> 单向哈希 -> 得到100bit的哈希值 -> 签名算法(利用私钥) -> 发送明文和签名 -> 比较明文的哈希值 和用公钥解密的签名

Message Authentication Code

keyed hash function 用的是共享的key, 不是公钥

Comments