7 经济增长理论
经济增长理论
增长率
\(g_z=\lim_{\delta t\to 0}\frac{z(t+\delta t)-z(t)}{z(t)}=\frac{d z(t)}{z(t)dt}=\boxed{\frac{d\ln z(t)}{dt}}\)
\(Z=XY\) 两边取对数对t求导, 则\(\boxed{g_{XY}=g_X+g_Y}\)
索洛增长理论(新古典增长模型)
模型结论 P272
内生变量: 劳动L, 资本K
没有技术进步
\(Y=F(K,L)\) Y实际产出 K资本 L劳动
规模报酬不变 \(\lambda Y=F(\lambda K,\lambda L)\)
边际产出为正,且边际产出递减
\(\frac{Y}{L}=F(\frac{K}{L},1)\) (设人均产出\(y=Y/L,k=K/L\). 因此对人均, \(y=F(k,1)=f(k)\)
考虑两部门经济,设储蓄率=投资率=\(s\) 平衡的时候\(I=S,S=sY\)
假设资本折旧率为\(\delta\),则 \(\dot{K}=I-\delta K=\boxed{sY-\delta K}\) (上面加点表示对时间求导)
假设人口增长率\(n=\frac{dL/dt}{L}\), 没有技术进步
那么人均资本积累\(\frac{d(K/L)}{dt}=\frac{\dot{K}L-K\dot{L}}{L^2}=\frac{sY-\delta K}{L}-\frac{K}{L}n=sf(k)-(\delta+n)k\)
解释: \(sf(k)\)是人均储蓄 \((\delta+n)k\)是"必要"的投资: 为了阻止人均资本k下降,需要\(\delta k\)来抵消折旧, \(nk\)来抵消人口增长对资本的影响
有技术进步
\(Y=F(AL,K)\) \(A\)代表技术进步 记\(\hat{y}=\frac{Y}{AL},\hat{k}=\frac{K}{AL}\) 表示按 有效劳动 平均的资本和产量, 而\(y=\frac{K}{L}\)是 人均
\(\hat{y}=f(\hat{k})\)
\(\frac{d\hat{k}}{dt}=\frac{\dot{K}AL-K(A\dot{L}+\dot{A}L)}{(AL)^2}=\frac{sY-\delta K}{AL}-\frac{K}{AL}(\frac{\dot{L}}{L}+\frac{\dot{A}}{A})\)
因此
稳态
课本P264-267
稳态 \(\dot{k}=0\)
稳态增长率: 分别考虑人均(小写字母) 和总量(大写字母)
人均资本\(\frac{K}{N}=\hat{k}A\) 显然增长率只取决于\(A\)
| 内生变量 | 稳态增长率(无技术进步) | 稳态增长率(有技术进步) |
|---|---|---|
| 人均资本\(k\) | 0 | \(g\) (等于技术进步速率) |
| 人均产量\(y\) | 0 | g |
| 总资本\(K\) | \(n\) (等于人口自然增长率) | g+n |
| 总产出\(Y\) | \(n\) (等于人口自然增长率) | g+n |
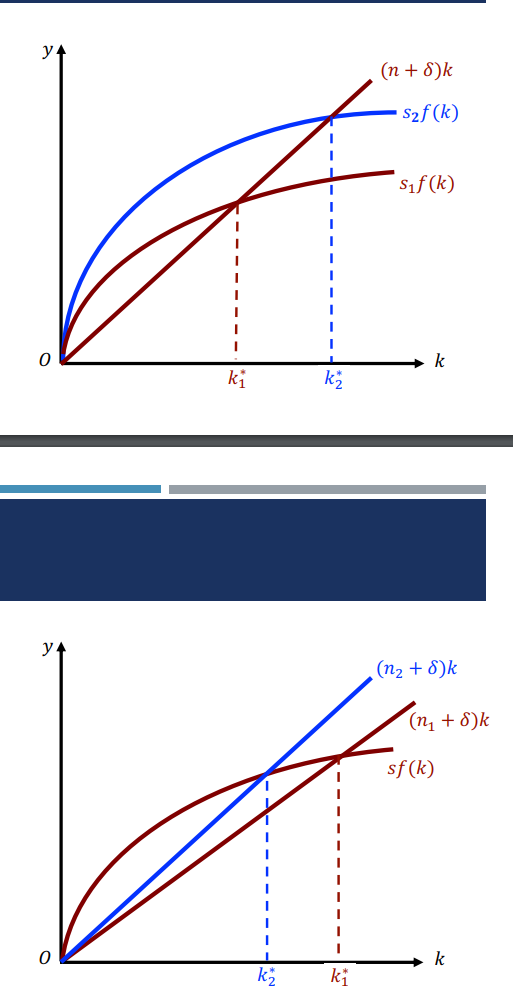
储蓄率增加, 收入稳态水平提高,但稳态增长率不变 (只有水平效应,没有增长效应)
人口增长率增加, 人均收入水平下降
资本黄金律水平
消费=\(f(k)-sf(k)\) 最大的\(k\).
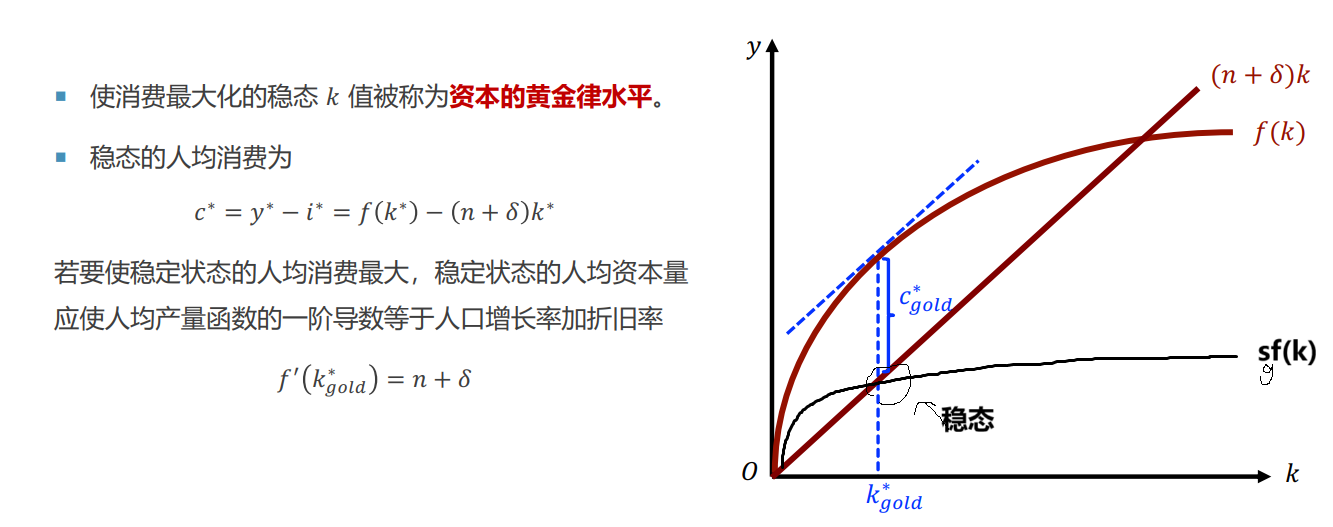
\(k_{gold}\)需要需要通过调整积累和消费政策, 以一个特定的储蓄率来支持它。储蓄率\(s_{gold}\)
含义:资本边际产出=人口增长率+折旧率
内生增长理论
不存在资本边际产出递减
经济增长核算
\(Y=AF(K,L)\) \(A\)是全要素生产率, 衡量技术水平
\(dY=F(K,L)dA+A\frac{\partial F}{\partial K}dK+A\frac{\partial F}{\partial L}dL\)
\(\frac{dY}{Y}=\frac{dA}{A}+\frac{MPK\cdot K}{F}\frac{dK}{K}+\frac{MPL\cdot L}{F}\frac{dL}{L}\)
又因为\(\lambda F(K,L)=F(\lambda K,\lambda L)\) 对\(\lambda\)求导得 \(F(K,L)=K\cdot MPK+L\cdot MPL\) 两个系数和为1. 因此可以写成
\(g_Y=g_A+ag_K+(1-a)g_L\)
实际上\(g_A\)是由其他量间接测出来的 \(g_A\)被称为索洛余量, 是全要素生产率的增长率
提高\(g_A\)的方法
- 鼓励资本形成
- 鼓励技术进步
- 建立适当的制度